Définition :
Le coefficient de corrélation de Pearson est la covariance de deux variables, divisée par le produit de leurs écarts-types. Cette définition implique un "moment produit", c'est-à-dire la moyenne (le premier moment par rapport à l'origine) du produit des variables aléatoires ajustées par leur moyenne ; d'où l'appellation moment-produit. Pour plus d'informations, consultez : https://fr.wikipedia.org/wiki/Coefficient_de_correlation_de_Pearson.
Cette version :
Cette version vous permet de calculer le coefficient sur le symbole actuel, ainsi que de déterminer le coefficient de corrélation entre deux symboles.
- Lorsque le paramètre "Deuxième symbole" est laissé vide, le symbole du graphique actuel est utilisé. Dans ce cas, le paramètre "Lag" doit être supérieur à 0, sinon le résultat sera toujours 0.
- Lorsque le paramètre "Deuxième symbole" est défini avec un symbole valide différent de celui du graphique actuel, ce symbole est utilisé. Dans ce cas, le paramètre "Lag" doit être réglé à 0 (pour calculer la corrélation des barres correspondantes), mais vous pouvez également introduire un lag, en gardant à l'esprit que les données du second symbole seront effectivement en retard dans ce cas.
Utilisation :
Comme tout indicateur de corrélation, lorsque la corrélation attendue dévie, cela peut servir de signal pour prendre des mesures appropriées (dans un style de trading basé sur la corrélation).
Exemples :
Symbole actuel avec un lag de 1 barre :
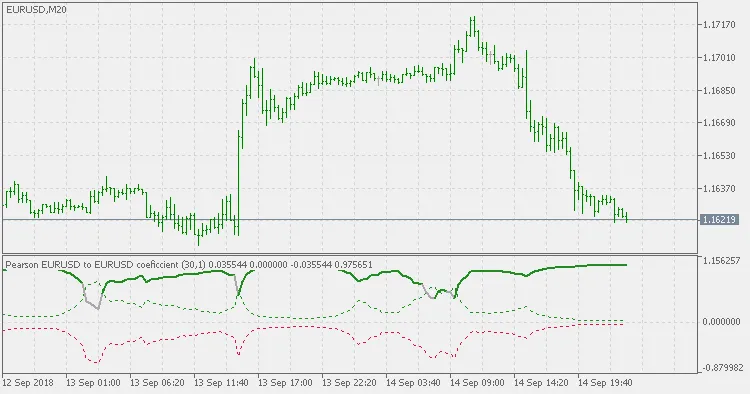
Symbole étranger avec un lag de 0 barre :
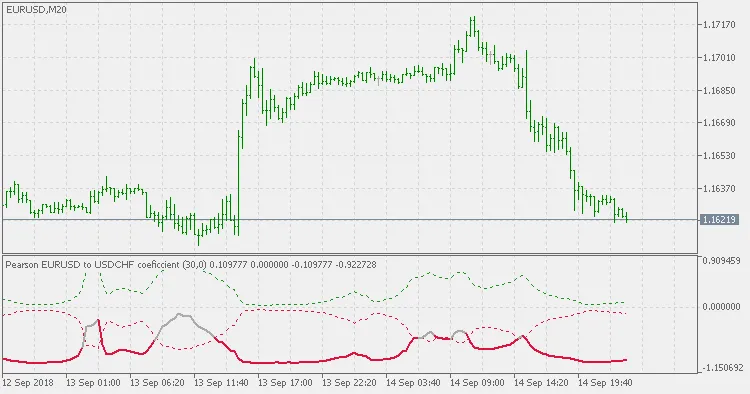

Commentaire 0