广义自回归条件异方差(GARCH)指标是基于GARCH(1,1)递归模型,用于预测金融资产价格波动性。这种统计模型在金融时间序列分析中非常常见,假设时间序列的方差是自相关的,并且误差项(模型预测与实际发生之间的差异)遵循一个自回归移动平均过程。由于金融市场的误差项变化通常不规则,因此被称为异方差性。
金融机构使用GARCH模型来估算股票、债券和市场指数的波动性。这个指标已经在外汇、商品(如黄金XAUUSD)和加密货币(如比特币BTCUSD)中进行了测试。
输入参数:
- 伽玛变量 - 常数项(无条件方差)
- 阿尔法变量 - ARCH系数(对最近冲击的反应)
- 贝塔变量 - 广义ARCH系数(过去方差的持续性)
- 条形窗口 - 包含在滚动均值/标准差中的条形数量
- 阈值比例 - 默认值为1。
线条说明:
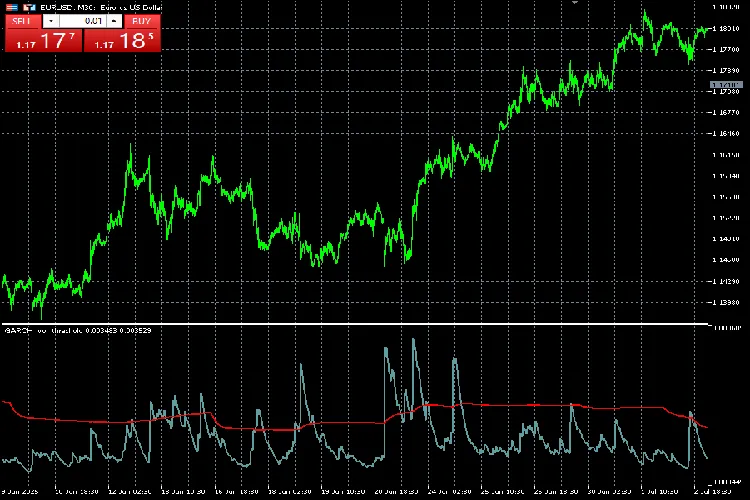
- 蓝色线条代表GARCH一阶预测值,即下一个蜡烛图的波动性(方差)。该线条是通过GARCH(1,1)公式计算的。在剧烈的回报变化期间,线条会急剧上升,然后缓慢回落到基线,表明这是一个高波动期。
- 红色线条表示高/低波动期的阈值。这使得交易者能够识别出两条线交叉信号,同时也便于专家顾问识别高度波动的区域。阈值比例也可以放大。
值得注意的是,这个指标在M1和M5时间框架下可能无法正常工作。
想了解更多关于GARCH的信息,可以访问:Investopedia GARCH

评论 0