Salut les traders ! Aujourd'hui, je vais vous parler d'un outil d'analyse très intéressant : l'indicateur de facteur d'uniformité. Cet indicateur, bien qu'il ne donne pas de signaux, a pour but de tester l'hypothèse que les séries temporelles des prix suivent une "marche aléatoire", en particulier une "marche aléatoire" gaussienne. Cela peut aider à transformer les variations de prix en séries temporelles uniformément distribuées, plus stables et prévisibles, au moins en termes de volatilité.
Comme vous le savez, la distance qu'une variable de "marche aléatoire" est censée parcourir après N étapes est estimée par son écart type multiplié par la racine carrée de N, ou N^0.5.
Ce qu'il faut savoir, c'est que cet indicateur calcule des statistiques sur le changement "moyen" des prix (par barre) pour des sous-ensembles de barres prédéfinis. Le "moyenne" est effectuée sur la distance (le nombre de barres jusqu'à N donné) porté à la puissance F — un facteur qui varie de 0.1 à 1 avec un pas de 0.1.
Toutes les barres disponibles sur le graphique actuel sont utilisées pour collecter des statistiques dans des fenêtres glissantes allant jusqu'à N barres.
Ensuite, l'indicateur recherche la distribution uniforme la plus "régulière" des statistiques parmi les différents F, et affiche un histogramme pour ce facteur (considéré comme optimal), généralement 0.5 ou 0.6. Chaque colonne de l'histogramme représente le delta "moyen" de points par barre pour une durée de trade correspondante (nombre de barres), où le "moyenne" est calculé par N^F (lorsque F=1, vous obtiendrez une moyenne standard).
L'indicateur peut utiliser différentes méthodes pour détecter automatiquement la "régularité" (aplatissement) de la courbe statistique :
- minimum de variance;
- minimum de différence entre les trois M (Moyenne, Médiane, Mode), en tant qu'erreur carrée;
- minimum du coefficient de Gini;
Savoir quel est le facteur optimal peut être utile pour :
- normaliser les données d'entrée (changements de prix) pour les réseaux neuronaux et d'autres algorithmes d'apprentissage automatique;
- estimer le nombre suffisant de barres pour un échantillonnage dans un seul vecteur d'entrée pour une analyse dans les systèmes de trading de volatilité;
- découvrir des symboles et/ou des périodes avec des anomalies (F non standard ou singularité dans la courbe de distribution);
Paramètres
- Période — distance maximale en barres (N) à utiliser pour collecter des statistiques sur la plage de prix, par défaut 200;
- Facteur — exposant pour la "moyenne" sur les distances, par défaut 0 - signifie autodétection, vous pouvez entrer une valeur personnalisée entre 0.0 et 1.0 pour l'estimation, par exemple, 0.525;
- Méthode — l'une des méthodes d'estimation de l'uniformité : variance, triple_M, Gini;
- MaxBars — une limite de barres à calculer pour les statistiques, par défaut 0 - signifie toutes les barres disponibles;
NB : Si vous utilisez un nombre illimité ou des centaines de milliers de barres sur le graphique, le calcul peut prendre un certain temps — si cela pose problème, envisagez de limiter le nombre de barres à des dizaines de milliers.
Résultats
L'indicateur affiche un histogramme bleu du changement moyen de prix par barre pour chaque distance dans la plage de distances (1..Période) et pour le facteur d'uniformité sélectionné.
Un nombre en constante augmentation de barres (distance) est également présenté sous forme de second histogramme (orange), juste pour référence.
Un tableau complet des facteurs testés et des métriques correspondantes de la série temporelle actuelle sont imprimés dans le log.
XAGUSD.c D1, Max.Distance: 500, Bars: 2641 Factor: 0.4, Result: var(0.4) mmm(0.4) gini(0.4)* [factor] [mean] [variance] [skewness] [kurtosis] [median] [mode] [mmmse] [gini] [0] 0.10000 1.85217 0.21976 -0.87694 0.07751 1.95822 2.30853 0.33811 0.13930 [1] 0.20000 1.07575 0.04083 -1.12699 0.96219 1.12715 1.25786 0.13285 0.10093 [2] 0.30000 0.62887 0.00525 -1.54472 3.00927 0.64878 0.68616 0.04114 0.05943 [3] 0.40000 0.37043 0.00021 -2.90499 13.36923 0.37546 0.37502 0.00394 0.01753 [4] 0.50000 0.22015 0.00028 1.53459 1.38333 0.21532 0.21461 0.00426 0.03779 [5] 0.60000 0.13222 0.00064 1.98696 4.05157 0.12372 0.10902 0.01661 0.09162 [6] 0.70000 0.08041 0.00072 2.60714 8.60950 0.07122 0.05862 0.01551 0.15135 [7] 0.80000 0.04964 0.00065 3.39070 15.85717 0.04099 0.03149 0.01289 0.21637 [8] 0.90000 0.03119 0.00054 4.37643 27.17457 0.02359 0.01692 0.01018 0.28652 [9] 1.00000 0.02002 0.00044 5.57319 43.86448 0.01358 0.00909 0.00787 0.36126
Captures d'Écran
Les captures d'écran suivantes montrent l'indicateur sur 3 périodes : D1, H1, M1.
Chaque graphique contient 2 instances de l'indicateur :
- la première est configurée pour l'autodétection du F par Gini, et la valeur trouvée (variant entre 0.4 une fois, et 0.5 deux fois) est affichée dans le titre, marquée par une astérisque;
- la deuxième est configurée pour un F prédéfini à 0.6;
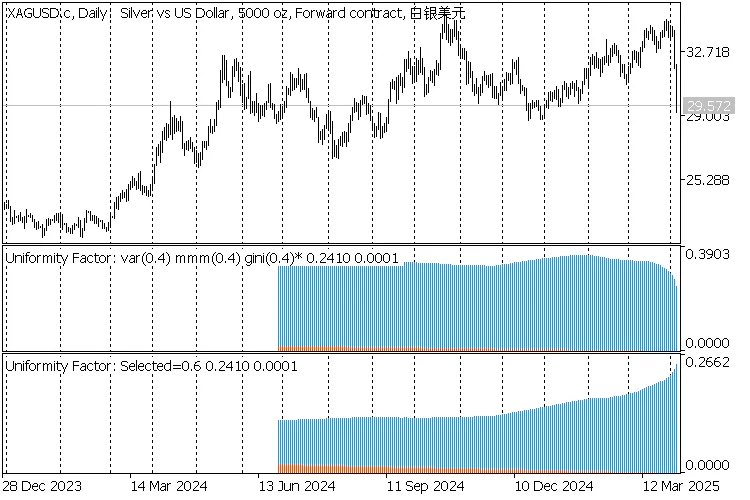
2 indicateurs de Facteur d'Uniformité sur XAGUSD,D1
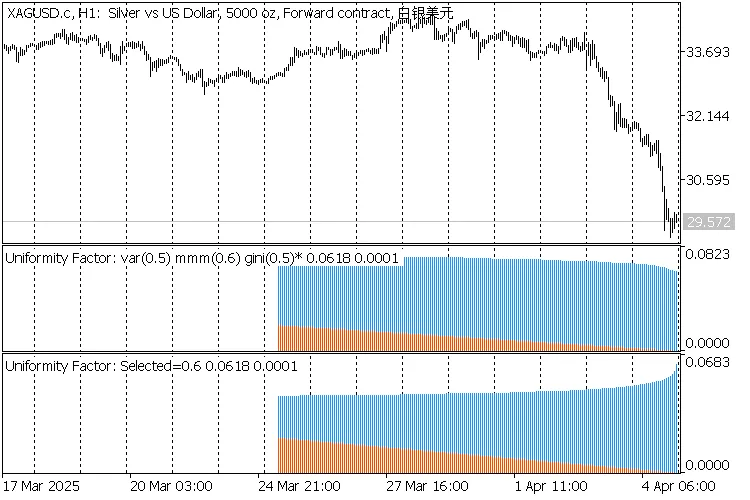
2 indicateurs de Facteur d'Uniformité sur XAGUSD,H1
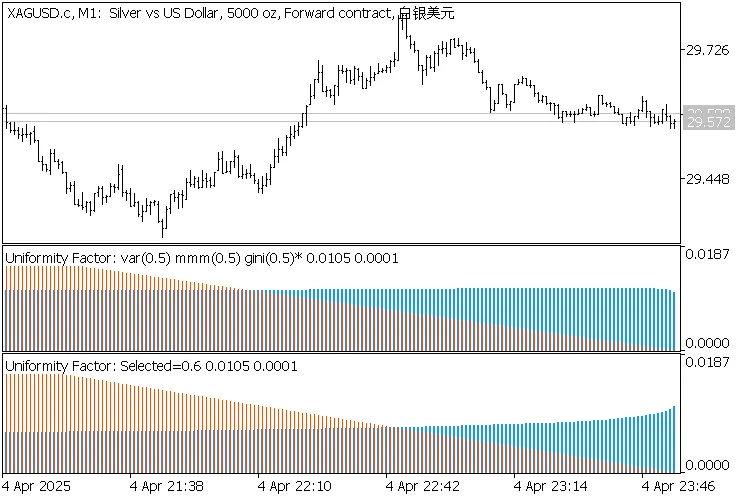
2 indicateurs de Facteur d'Uniformité sur XAGUSD,M1
Articles connexes
- iMAX3 : Détecteur de Tendances Rapides pour Traders
- Découvrez l'indicateur Tymen STARC Bands MTF pour MetaTrader 5
- Affichez la tendance actuelle sur tous les délais avec un indicateur pour MetaTrader 4
- Améliorez vos graphiques avec ClearView : Indicateurs et modèles pour MetaTrader 5
- Découvrez l'indicateur 3 en 1 Stochastic pour MetaTrader 5