Hey there, fellow traders!
Today, I’m excited to share with you my creation: the FE Fibonacci Expansion indicator for MetaTrader 4. This nifty tool is designed using two objects in an array that represent properties for two directions: UP and DOWN.
How It Works
Let's break it down. Each direction will have three prices: A, B, and C, which correspond to the upper, lower, and mid-range prices. The variables aa, bb, and cc indicate the bar locations for their respective prices.
class FEExpansion
{
public:
int aa, bb, cc;
double A, B, C;
FEExpansion():
aa(0), bb(0), cc(0),
A(0.0), B(0.0), C(0.0)
{}
~FEExpansion() {}
} P[2];
Each direction is determined using a fractal formula with a bit of tweaking to pinpoint the three key points: upper, lower, and a price in between, all along with their directions.
Looping Through Bars
Here’s how I loop through the recent bar locations:
//---
int i=0;
int m=0, n=0;
bool stop=false;
double hi=0.0, lo=0.0;
//---
A=0.0;
B=0.0;
C=0.0;
for(m=0, n=0, i=0; i<Bars-5&&!stop; i++)
{
hi=(
iHigh(_Symbol,0,i+2)>=iHigh(_Symbol,0,i+0) &&
iHigh(_Symbol,0,i+2)>=iHigh(_Symbol,0,i+1) &&
iHigh(_Symbol,0,i+2)>=iHigh(_Symbol,0,i+3) &&
iHigh(_Symbol,0,i+2)>=iHigh(_Symbol,0,i+4))
?iHigh(_Symbol,0,i+2):0.0;
lo=(
iLow(_Symbol,0,i+2)<=iLow(_Symbol,0,i+0) &&
iLow(_Symbol,0,i+2)<=iLow(_Symbol,0,i+1) &&
iLow(_Symbol,0,i+2)<=iLow(_Symbol,0,i+3) &&
iLow(_Symbol,0,i+2)<=iLow(_Symbol,0,i+4))
?iLow(_Symbol,0,i+2):0.0;
//---
//---
//--------------------------------------------------------------------------------------------------------------------
//--------------------------------------------------------------------------------------------------------------------
if(hi!=0.0)// ------------up------------
{
if(P[1].C!=0.0)
{
if(n==2)
{
if(P[1].B<hi&&P[1].C<P[1].B)
{
P[1].B=hi; //this modify B[1] before A[1] exist
P[1].bb=i+2;
}
if(n==1)
{
if(P[1].C<hi)
{
P[1].B=hi; //this B[1] dn
P[1].bb=i+2;
n++;
}
else
{
n--;
P[1].C=0.0;
}
}
}
//---
if(P[0].C==0.0)
{
if(m<1)
{
P[0].C=hi; //initial C[0] up
P[0].cc=i+2;
m++;
}
}
else
{
if(m==2)
{
if(P[0].C<hi)
{
P[0].A=hi; //this A[0] up
P[0].aa=i+2;
m=0;
stop=true;
}
}
if(m==1)
{
if(P[0].C<hi)
{
P[0].C=hi; //this modify C[0] before B[0] exist
P[0].cc=i+2;
}
}
}
//---
}
//else
if(lo!=0.0)// ------------dn------------
{
if(P[0].C!=0.0)
{
if(m==2)
{
if(P[0].B>lo&&P[0].C>P[0].B)
{
P[0].B=lo; //this modify B[0] before A[0] exist
P[0].bb=i+2;
}
}
if(m==1)
{
if(P[0].C>lo)
{
P[0].B=lo; //this B[0] up
P[0].bb=i+2;
m++;
}
else
{
m--;
P[0].C=0.0;
}
}
}
//---
if(P[1].C==0.0)
{
if(n<1)
{
P[1].C=lo; //initial C[1] dn
P[1].cc=i+2;
n++;
}
}
else
{
if(n==2)
{
if(P[1].C>lo)
{
P[1].A=lo; //this A[1] dn
P[1].aa=i+2;
n=0;
stop=true;
}
}
if(n==1)
{
if(P[1].C>lo)
{
P[1].C=lo; //this modify C[1] before B[1] exist
P[1].cc=i+2;
}
}
}
}
//---
}
//else
//
//---
//---
//---
if((P[0].C==0.0&&P[1].C==0.0)||(hi==0.0&&lo==0.0))
{
continue;
}
}
// loop
If the loop finds three points indicating either an upward or downward direction, it breaks out of the loop.
Finalizing the Expansion
Now, let’s pull out the three points:
if(P[0].A!=0.0&&P[0].B!=0.0&&P[0].C!=0.0)
{
DrawExpansion(tool,"FE ->",Time[P[0].aa],P[0].A,Time[P[0].bb],P[0].B,Time[P[0].cc],P[0].C,-1);
}
//---
if(P[1].A!=0.0&&P[1].B!=0.0&&P[1].C!=0.0)
{
DrawExpansion(tool,"FE ->",Time[P[1].aa],P[1].A,Time[P[1].bb],P[1].B,Time[P[1].cc],P[1].C,1);
}
Finally, we use the OBJ_EXPANSION object to draw our expansion with a single function call, DrawExpansion(...).
void DrawExpansion(string name,string label,datetime t1,double p1,datetime t2,double p2,datetime t3,double p3,int fl=0)
{
//---
ObjectDelete(name);
color wrn=(fl>0)?clrSkyBlue:(fl<0)?clrTomato:clrWhite;
if(ObjectFind(0,name)!=0)
ObjectCreate(name,OBJ_EXPANSION,0,t1,p1,t2,p2,t3,p3);
ObjectSet(name,OBJPROP_FIBOLEVELS,5);
ObjectSet(name,OBJPROP_FIRSTLEVEL+0,0.618);
ObjectSet(name,OBJPROP_FIRSTLEVEL+1,1.000);
ObjectSet(name,OBJPROP_FIRSTLEVEL+2,1.618);
ObjectSet(name,OBJPROP_FIRSTLEVEL+3,2.618);
ObjectSet(name,OBJPROP_FIRSTLEVEL+4,4.236);
//---
ObjectSet(name,OBJPROP_LEVELCOLOR,clrMediumPurple);
ObjectSet(name,OBJPROP_LEVELWIDTH,1);
ObjectSet(name,OBJPROP_LEVELSTYLE,0);
ObjectSet(name,OBJPROP_COLOR,wrn);
//---
ObjectSetFiboDescription(name,0,label+" "+DoubleToStr(0.618*100,1" ");
ObjectSetFiboDescription(name,1,label+" "+DoubleToStr(1.000*100,1" ");
ObjectSetFiboDescription(name,2,label+" "+DoubleToStr(1.618*100,1" ");
ObjectSetFiboDescription(name,3,label+" "+DoubleToStr(2.618*100,1" ");
ObjectSetFiboDescription(name,4,label+" "+DoubleToStr(4.236*100,1" ");
//---
}
In this function, I set levels at 0.618, 1.000, 1.618, 2.618, and 4.236, creating a comprehensive Fibonacci expansion.
Here’s a quick glance at what it looks like:
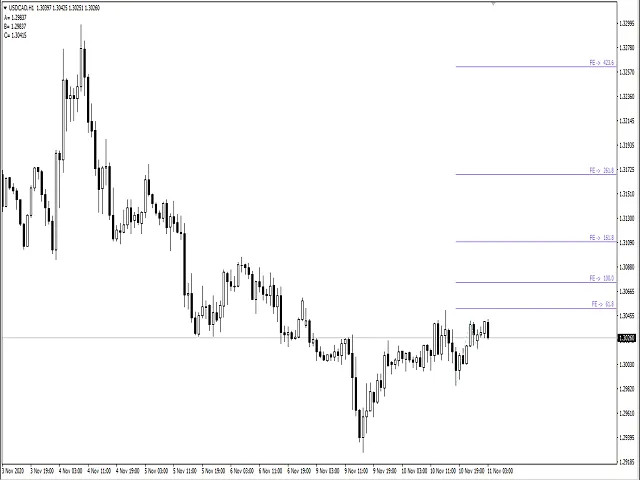
In Conclusion: The FE Fibonacci Expansion indicator is a powerful tool for traders looking to make informed decisions based on Fibonacci levels. Give it a try in your trading strategy!
Related Posts
- Unlock Trading Insights with Volume Profile + Range v6.0 for MetaTrader 5
- Hourly Buffers for Data Collection in MetaTrader 5: A Simple Guide
- Mastering the MACD Candle Indicator for MetaTrader 4
- Unlocking MetaCOT 2: Your Ultimate CFTC Indicator Toolkit for MT4
- Master Your Trading with ACC+BAL+MARG-INDI for MetaTrader 4