Memprediksi Harga Selanjutnya dengan Jaringan Saraf: Panduan Lengkap untuk Trader -

Penulis: gpwr

Riwayat Versi:

26/06/2009 - menambahkan indikator baru BPNN Predictor dengan Smoothing.mq4, di mana harga diperhalus menggunakan EMA sebelum prediksi.

20/08/2009 - memperbaiki kode yang menghitung fungsi aktivasi neuron untuk mencegah pengecualian aritmatika; memperbarui BPNN.cpp dan BPNN.dll.

21/08/2009 - menambahkan pembersihan memori di akhir eksekusi DLL; memperbarui BPNN.cpp dan BPNN.dll.

Teori Singkat Jaringan Saraf:

Jaringan saraf adalah model yang dapat disesuaikan dari keluaran sebagai fungsi dari masukan. Model ini terdiri dari beberapa lapisan:

lapisan masukan, yang terdiri dari data masukan
lapisan tersembunyi, yang terdiri dari node pemrosesan yang disebut neuron
lapisan keluaran, yang terdiri dari satu atau beberapa neuron, yang keluaran tersebut adalah keluaran jaringan.

Semua node dari lapisan yang berdekatan saling terhubung. Koneksi ini disebut sinapsis. Setiap sinapsis memiliki koefisien skala yang ditugaskan, di mana data yang dipropagasikan melalui sinapsis dikalikan. Koefisien skala ini disebut bobot (w[i][j][k]). Dalam Jaringan Saraf Maju (Feed-Forward Neural Network) (FFNN), data dipropagasikan dari masukan ke keluaran. Berikut adalah contoh FFNN dengan satu lapisan masukan, satu lapisan keluaran, dan dua lapisan tersembunyi:

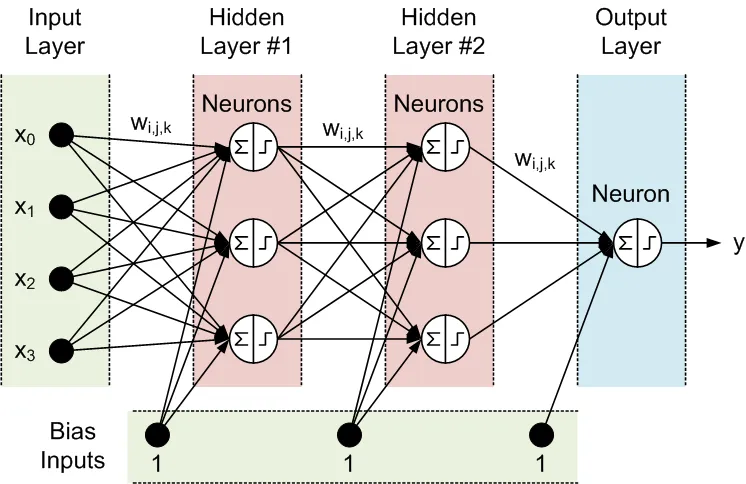
Topologi dari FFNN sering disingkat sebagai berikut: <# masukan> - <# neuron di lapisan tersembunyi pertama> - <# neuron di lapisan tersembunyi kedua> -...- <# keluaran>. Jaringan di atas dapat disebut sebagai jaringan 4-3-3-1.

Data diproses oleh neuron dalam dua langkah, sesuai yang ditunjukkan dalam lingkaran dengan tanda penjumlahan dan tanda langkah:

Semua masukan dikalikan dengan bobot terkait dan dijumlahkan.
Jumlah yang dihasilkan diproses oleh fungsi aktivasi neuron, yang keluaran adalah keluaran neuron.

Fungsi aktivasi neuron memberikan non-linearitas pada model jaringan saraf. Tanpa itu, tidak ada alasan untuk memiliki lapisan tersembunyi, dan jaringan saraf menjadi model autoregressive linier (AR).

File perpustakaan yang dilampirkan untuk fungsi NN memungkinkan pemilihan antara tiga fungsi aktivasi:

sigmoid sigm(x)=1/(1+exp(-x)) (#0)
tangen hiperbolik tanh(x)=(1-exp(-2x))/(1+exp(-2x)) (#1)
fungsi rasional x/(1+|x|) (#2)

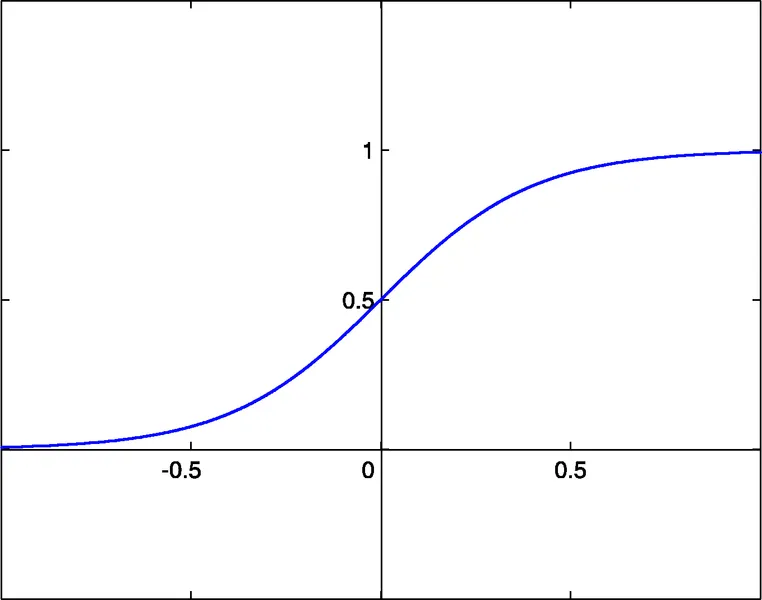
Ambang aktivasi dari fungsi-fungsi ini adalah x=0. Ambang ini dapat dipindahkan di sepanjang sumbu x berkat masukan tambahan dari setiap neuron, yang disebut masukan bias, yang juga memiliki bobot yang ditugaskan.

Jumlah masukan, keluaran, lapisan tersembunyi, neuron di lapisan ini, dan nilai bobot sinapsis sepenuhnya menggambarkan sebuah FFNN, yaitu model non-linear yang diciptakannya. Untuk menemukan bobot, jaringan harus dilatih. Selama pelatihan terawasi, beberapa set masukan masa lalu dan keluaran yang diharapkan dimasukkan ke dalam jaringan. Bobot dioptimalkan untuk mencapai kesalahan terkecil antara keluaran jaringan dan keluaran yang diharapkan. Metode paling sederhana untuk optimasi bobot adalah back-propagation dari kesalahan, yang merupakan metode penurunan gradien. Fungsi pelatihan yang dilampirkan Train() menggunakan varian dari metode ini, yang disebut Improved Resilient back-Propagation Plus (iRProp+).

http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.17.1332

Kekurangan utama dari metode optimasi berbasis gradien adalah bahwa mereka sering menemukan minimum lokal. Untuk seri yang kacau seperti seri harga, permukaan kesalahan pelatihan memiliki bentuk yang sangat kompleks dengan banyak minimum lokal. Untuk seri semacam ini, algoritma genetik adalah metode pelatihan yang lebih disukai.

File yang dilampirkan:

BPNN.dll - file perpustakaan
BPNN.zip - arsip semua file yang diperlukan untuk mengompilasi BPNN.dll dalam C++
BPNN Predictor.mq4 - indikator yang memprediksi harga buka di masa depan
BPNN Predictor dengan Smoothing.mq4 - indikator yang memprediksi harga buka yang diperhalus

File BPNN.cpp memiliki dua fungsi: Train() dan Test(). Train() digunakan untuk melatih jaringan berdasarkan nilai masukan dan keluaran yang diharapkan. Test() digunakan untuk menghitung keluaran jaringan menggunakan bobot yang dioptimalkan, yang ditemukan oleh Train().

Berikut adalah daftar parameter masukan (hijau) dan keluaran (biru) dari Train():

double inpTrain[] - Data pelatihan masukan (array 1D yang membawa data 2D, yang lebih tua pertama)
double outTarget[] - Data target keluaran untuk pelatihan (data 2D sebagai array 1D, yang lebih tua pertama)
double outTrain[] - Array keluaran 1D untuk menampung keluaran jaringan dari pelatihan
int ntr - # set pelatihan
int UEW - Gunakan Bobot Eksternal untuk inisialisasi (1=gunkan extInitWt, 0=gunkan rnd)
double extInitWt[] - Array masukan 1D untuk menampung array 3D dari bobot inisialisasi eksternal
double trainedWt[] - Array keluaran 1D untuk menampung array 3D dari bobot terlatih
int numLayers - # lapisan termasuk masukan, tersembunyi dan keluaran
int lSz[] - # neuron di lapisan. lSz[0] adalah # masukan net
int AFT - Jenis fungsi aktivasi neuron (0:sigm, 1:tanh, 2:x/(1+x))
int OAF - 1 mengaktifkan fungsi aktivasi untuk lapisan keluaran; 0 menonaktifkan
int nep - Max # epoch pelatihan
double maxMSE - Max MSE; pelatihan berhenti setelah maxMSE tercapai

Berikut adalah daftar parameter masukan (hijau) dan keluaran (biru) dari Test():

double inpTest[] - Data pengujian masukan (data 2D sebagai array 1D, yang lebih tua pertama)
double outTest[] - Array keluaran 1D untuk menampung keluaran jaringan dari pelatihan (yang lebih tua pertama)
int ntt - # set pengujian
double extInitWt[] - Array masukan 1D untuk menampung array 3D dari bobot inisialisasi eksternal
int numLayers - # lapisan termasuk masukan, tersembunyi dan keluaran
int lSz[] - # neuron di lapisan. lSz[0] adalah # masukan net
int AFT - Jenis fungsi aktivasi neuron (0:sigm, 1:tanh, 2:x/(1+x))
int OAF - 1 mengaktifkan fungsi aktivasi untuk lapisan keluaran; 0 menonaktifkan

Apakah akan menggunakan fungsi aktivasi di lapisan keluaran atau tidak (nilai parameter OAF) tergantung pada sifat keluaran. Jika keluaran bersifat biner, yang sering terjadi dalam masalah klasifikasi, maka fungsi aktivasi harus digunakan di lapisan keluaran (OAF=1). Harap diperhatikan bahwa fungsi aktivasi #0 (sigmoid) memiliki level jenuh 0 dan 1, sementara fungsi aktivasi #1 dan #2 memiliki level -1 dan 1. Jika keluaran jaringan adalah prediksi harga, maka tidak perlu fungsi aktivasi di lapisan keluaran (OAF=0).

Contoh Penggunaan Perpustakaan NN:

BPNN Predictor.mq4 - memprediksi harga buka di masa depan. Masukan jaringan adalah perubahan harga relatif:

x[i]=Buka[test_bar]/Buka[test_bar+delay[i]]-1.0

di mana delay[i] dihitung sebagai angka Fibonacci (1,2,3,5,8,13,21..). Keluaran jaringan adalah perubahan relatif yang diprediksi dari harga berikutnya. Fungsi aktivasi dimatikan di lapisan keluaran (OAF=0).

Masukan indikator:

extern int lastBar - Bar terakhir dalam data masa lalu
extern int futBars - # bar masa depan untuk diprediksi
extern int numLayers - # lapisan termasuk masukan, tersembunyi & keluaran (2..6)
extern int numInputs - # masukan
extern int numNeurons1 - # neuron di lapisan tersembunyi pertama atau lapisan keluaran
extern int numNeurons2 - # neuron di lapisan tersembunyi kedua atau lapisan keluaran
extern int numNeurons3 - # neuron di lapisan tersembunyi ketiga atau lapisan keluaran
extern int numNeurons4 - # neuron di lapisan tersembunyi keempat atau lapisan keluaran
extern int numNeurons5 - # neuron di lapisan tersembunyi kelima atau lapisan keluaran
extern int ntr - # set pelatihan
extern int nep - Max # epoch
extern int maxMSEpwr - menetapkan maxMSE=10^maxMSEpwr; pelatihan berhenti < maxMSE
extern int AFT - Jenis fungsi aktivasi (0:sigm, 1:tanh, 2:x/(1+x))

Indikator ini menggambar tiga kurva di grafik:

warna merah - prediksi harga masa depan
warna hitam - harga buka pelatihan masa lalu, yang digunakan sebagai keluaran yang diharapkan untuk jaringan
warna biru - keluaran jaringan untuk masukan pelatihan

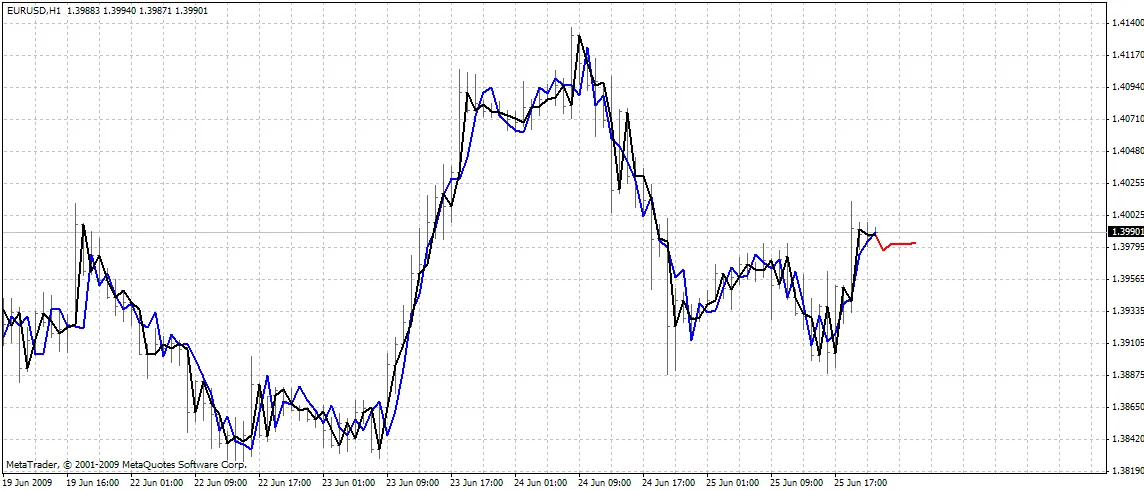
BPNN Predictor.mq4 - memprediksi harga buka yang diperhalus di masa depan. Menggunakan perhalusan EMA dengan periode smoothPer.

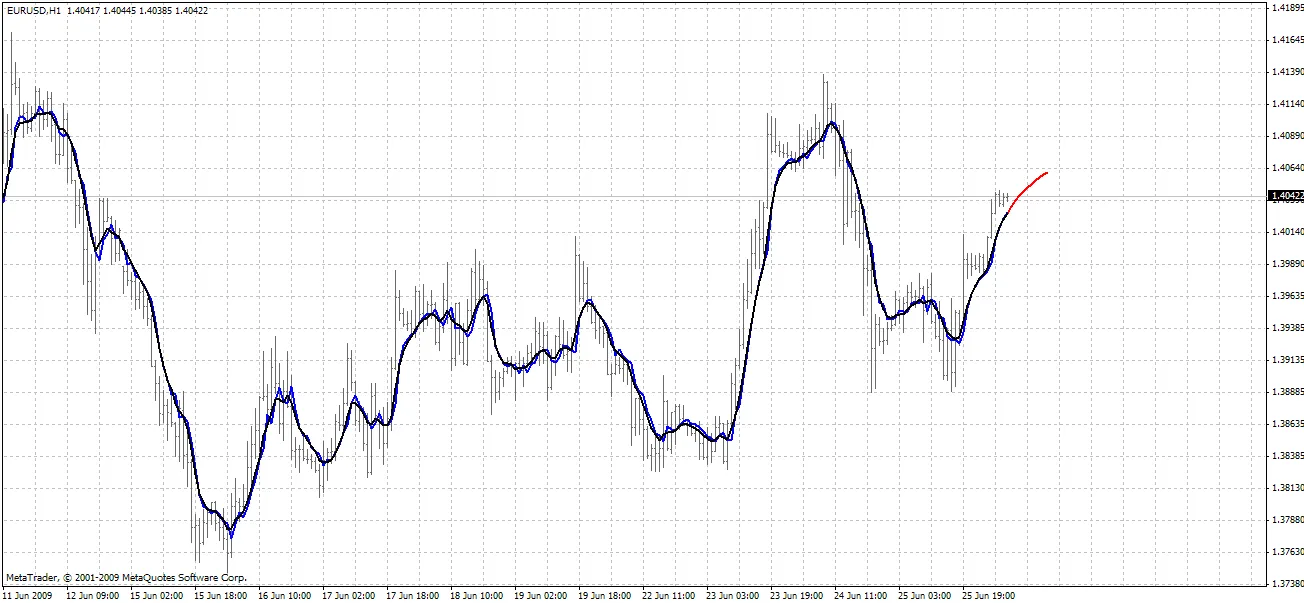
Pengaturan Semua:

Salin BPNN.DLL yang dilampirkan ke C:\Program Files\MetaTrader 4\experts\libraries
Di MetaTrader: Alat - Opsi - Penasihat Ahli - Izinkan impor DLL

Anda juga dapat mengompilasi file DLL Anda sendiri menggunakan kode sumber dalam BPNN.zip.

Rekomendasi:

Sebuah jaringan dengan tiga lapisan (numLayers=3: satu masukan, satu tersembunyi dan satu keluaran) sudah cukup untuk sebagian besar kasus. Menurut Teorema Cybenko (1989), jaringan dengan satu lapisan tersembunyi mampu mendekati fungsi multivariabel kontinu dengan tingkat akurasi yang diinginkan; jaringan dengan dua lapisan tersembunyi mampu mendekati fungsi multivariabel diskontinu.
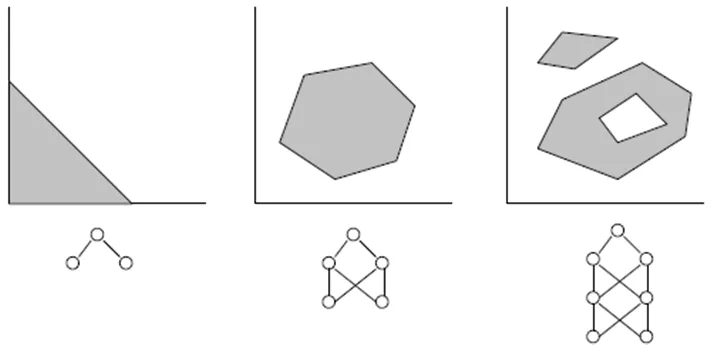
Jumlah neuron optimum di lapisan tersembunyi dapat ditemukan melalui percobaan dan kesalahan. "Aturan praktis" yang dapat ditemukan dalam literatur: # neuron tersembunyi = (# masukan + # keluaran)/2, atau SQRT(# masukan * # keluaran). Pantau kesalahan pelatihan, yang dilaporkan oleh indikator di jendela ahli MetaTrader.
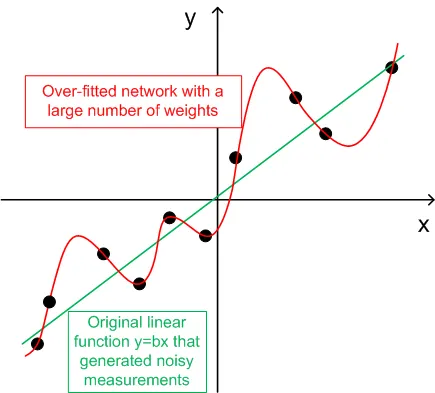
Untuk generalisasi, jumlah set pelatihan (ntr) harus dipilih 2-5 kali jumlah total bobot dalam jaringan. Sebagai contoh, secara default, BPNN Predictor.mq4 menggunakan jaringan 12-5-1. Jumlah total bobot adalah (12+1)*5+6=71. Oleh karena itu, jumlah set pelatihan (ntr) harus setidaknya 142. Konsep generalisasi dan memorisasi (overfitting) dijelaskan pada grafik di bawah ini.
Data masukan ke jaringan harus ditransformasikan menjadi stasioner. Harga Forex tidak stasioner. Sangat disarankan untuk menormalkan masukan ke rentang -1..+1.

Grafik di bawah menunjukkan fungsi linier y=b*x (x-masukan, y-keluaran) yang keluaran nya terganggu oleh noise. Noise yang ditambahkan menyebabkan keluaran fungsi yang diukur (titik hitam) menyimpang dari garis lurus. Fungsi y=f(x) dapat dimodelkan oleh jaringan saraf maju. Jaringan dengan sejumlah bobot besar dapat disesuaikan dengan data yang diukur dengan kesalahan nol. Perilakunya ditunjukkan sebagai kurva merah yang melewati semua titik hitam. Namun, kurva merah ini tidak ada hubungannya dengan fungsi linier asli y=b*x (hijau). Ketika jaringan yang overfitted ini digunakan untuk memprediksi nilai masa depan dari fungsi y(x), itu akan menghasilkan kesalahan besar karena sifat acak dari noise yang ditambahkan.

Sebagai imbalan untuk berbagi kode ini, penulis memiliki sedikit permohonan. Jika Anda berhasil membuat sistem perdagangan yang menguntungkan berdasarkan kode ini, silakan bagikan ide Anda kepada saya dengan mengirimkan email langsung ke vlad1004@yahoo.com.

Semoga sukses!

Memprediksi Harga Selanjutnya dengan Jaringan Saraf: Panduan Lengkap untuk Trader

Contoh Penggunaan Perpustakaan NN:

Postingan terkait