Média Móvel Adaptativa (AMA): O Indicador que Todo Trader Deve Conhecer

A Média Móvel Adaptativa (AMA) é um indicador incrível que nos ajuda a construir uma média móvel com baixa sensibilidade a ruídos nos preços e é conhecida por ter um atraso mínimo na detecção de tendências.

Desenvolvido por Perry Kaufman e descrito no seu livro "Smarter Trading", o AMA é uma ferramenta valiosa para traders que buscam melhorar suas análises.

Um dos grandes desafios com os algoritmos de suavização tradicionais é que saltos acidentais nos preços podem gerar sinais de tendência falsos. Por outro lado, a suavização pode causar um atraso inevitável nas previsões de tendências. O AMA foi criado para superar essas desvantagens.

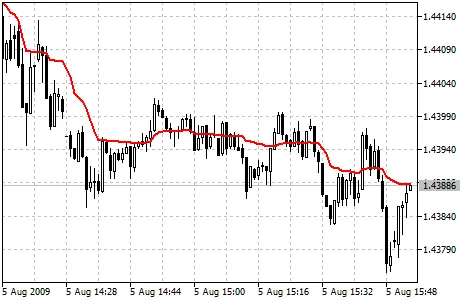
Indicador Média Móvel Adaptativa

Cálculo:

Para definir o estado atual do mercado, Kaufman introduziu o conceito de Razão de Eficiência (ER), que é calculada pela fórmula abaixo:

onde:

• ER(i) - valor atual da Razão de Eficiência;
• Sinal(i) = ABS(Preço(i) - Preço(i - N)) - valor atual do sinal, valor absoluto da diferença entre o preço atual e o preço de N períodos atrás;
• Ruído(i) = Soma(ABS(Preço(i) - Preço(i-1)),N) - valor atual do ruído, soma dos valores absolutos da diferença entre o preço do período atual e o preço do período anterior para N períodos.
  

Em uma tendência forte, a Razão de Eficiência (ER) tende a 1; se não houver movimento direcionado, será um pouco mais que 0.

O valor obtido de ER é utilizado na fórmula de suavização exponencial:

onde:

• SC = 2/(n+1) - constante de suavização EMA, n - período da média móvel exponencial;
• EMA(i-1) - valor anterior da EMA.

A razão de suavização para um mercado em movimento deve ser a mesma que a da EMA com período 2 (SC rápido = 2/(2+1) = 0.6667), e para o período sem tendência, a EMA deve ser igual a 30 (SC lento = 2/(30+1) = 0.06452). Assim, introduzimos uma nova constante de suavização variável (constante de suavização escalonada) SSC:

ou

Para uma influência mais eficiente da constante de suavização obtida no período de média, Kaufman recomenda elevá-la ao quadrado.

Fórmula de cálculo final:

ou (após rearranjo):

onde:

• AMA(i) - valor atual da AMA;
• AMA(i-1) - valor anterior da AMA;
• SSC(i) - valor atual da constante de suavização escalonada.