Fractal Adaptive Moving Average (FrAMA) adalah indikator teknikal yang dikembangkan oleh John Ehlers. Indikator ini sangat berguna bagi trader yang ingin memanfaatkan pergerakan harga yang kuat.
FrAMA dibangun berdasarkan algoritma dari Exponential Moving Average (EMA), di mana faktor pelunakan dihitung berdasarkan dimensi fraktal harga saat ini. Keunggulan dari FrAMA adalah kemampuannya untuk mengikuti pergerakan tren yang kuat, sekaligus melambat pada saat konsolidasi harga.
Berbagai jenis analisis yang digunakan untuk Moving Averages juga dapat diterapkan pada indikator ini.
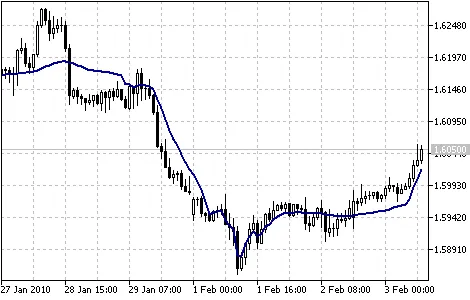
Indikator Fractal Adaptive Moving Average
Perhitungan:
FRAMA(i) = A(i) * Price(i) + (1 - A(i)) * FRAMA(i-1)
Di mana:
- FRAMA(i) - nilai FrAMA saat ini;
- Price(i) - harga saat ini;
- FRAMA(i-1) - nilai FrAMA sebelumnya;
- A(i) - faktor pelunakan eksponensial saat ini.
Faktor pelunakan eksponensial dihitung berdasarkan rumus berikut:
A(i) = EXP(-4.6 * (D(i) - 1))
Di mana:
- D(i) - dimensi fraktal saat ini;
- EXP() - fungsi matematis eksponensial.
Dimensi fraktal dari garis lurus adalah satu. Dari rumus tersebut, jika D = 1, maka A = EXP(-4.6 * (1-1)) = EXP(0) = 1. Artinya, jika harga bergerak dalam garis lurus, pelunakan eksponensial tidak digunakan, karena dalam hal ini rumusnya menjadi:
FRAMA(i) = 1 * Price(i) + (1 - i) * FRAMA(i-1) = Price(i)
Dengan kata lain, indikator ini akan mengikuti harga dengan tepat.
Dimensi fraktal dari bidang adalah dua. Dari rumus kita dapatkan jika D = 2, maka faktor pelunakan A = EXP(-4.6*(2-1)) = EXP(-4.6) = 0.01. Nilai kecil dari faktor pelunakan eksponensial ini diperoleh pada saat harga bergerak dengan pola zig-zag yang kuat. Pelunakan yang kuat ini setara dengan sekitar 200-period simple moving average.
Rumus dimensi fraktal:
D = (LOG(N1 + N2) - LOG(N3))/LOG(2)
Dihitung berdasarkan rumus tambahan:
N(Length,i) = (HighestPrice(i) - LowestPrice(i))/Length
Di mana:
- HighestPrice(i) - nilai maksimal saat ini untuk periode Length;
- LowestPrice(i) - nilai minimal saat ini untuk periode Length;
Nilai N1, N2, dan N3 masing-masing adalah:
N1(i) = N(Length,i)
N2(i) = N(Length,i + Length)
N3(i) = N(2 * Length,i)

Komentar 0