สวัสดีครับเพื่อนนักเทรดทุกคน! วันนี้เรามาพูดถึง ตัวชี้วัดปัจจัยความสม่ำเสมอ (Uniformity Factor Indicator) ซึ่งเป็นเครื่องมือวิเคราะห์ที่ช่วยให้เราทดสอบสมมติฐานว่าลำดับราคามีลักษณะเป็น "การเดินแบบสุ่ม" (random walk) โดยเฉพาะอย่างยิ่งเป็นการเดินแบบสุ่มแบบ Gaussian ซึ่งสามารถช่วยให้เราสร้างการแปลงพารามิเตอร์ของการเปลี่ยนแปลงราคาให้มีการกระจายอย่างสม่ำเสมอและมีความคาดการณ์ได้มากขึ้นในแง่ของความผันผวน
ตามที่หลายๆ คนอาจทราบกันดีว่า ระยะทางที่ตัวแปร "การเดินแบบสุ่ม" คาดว่าจะครอบคลุมหลังจากที่เดินไป N ขั้น สามารถประมาณได้จากการคูณส่วนเบี่ยงเบนมาตรฐาน (standard deviation) กับ sqrt(N) หรือ N^0.5
ตัวชี้วัดนี้จะคำนวณสถิติการเปลี่ยนแปลงราคาที่ "เฉลี่ย" (average) ต่อแท่ง (per bar) สำหรับช่วงของแท่งที่กำหนดไว้ โดยการ "เฉลี่ย" จะดำเนินการตามระยะห่าง (จำนวนแท่งที่ขึ้นอยู่กับ N) ที่ยกกำลัง F — ซึ่งเป็นปัจจัยที่นับจาก 0.1 ถึง 1 โดยมีขั้นตอน 0.1
แท่งทั้งหมดที่มีในกราฟปัจจุบันจะถูกใช้ในการเก็บสถิติในหน้าต่างเลื่อน (sliding windows) ของแท่งสูงสุดถึง N แท่ง
จากนั้น ตัวชี้วัดจะค้นหาการกระจายที่ "สม่ำเสมอ" ที่สุดของสถิติระหว่าง F ต่างๆ และแสดงฮิสโตแกรมสำหรับปัจจัยนี้ (ซึ่งถือว่าเหมาะสม) โดยปกติจะอยู่ที่ 0.5 หรือ 0.6 โดยแต่ละคอลัมน์ในฮิสโตแกรมจะแสดง "เฉลี่ย" ของการเปลี่ยนแปลงจุดต่อแท่งสำหรับระยะเวลาการเทรดที่สอดคล้องกัน (จำนวนแท่ง) ซึ่ง "การเฉลี่ย" จะทำโดย N^F (เมื่อ F=1 จะได้การเฉลี่ยตามปกติ)
ตัวชี้วัดนี้สามารถใช้วิธีการต่างๆ ในการตรวจจับ "ความสม่ำเสมอ" (regularity) ของกราฟสถิติ:
- ขั้นต่ำของความแปรปรวน;
- ขั้นต่ำของความแตกต่างระหว่าง M สามตัว (Mean, Median, Mode) ในรูปแบบของข้อผิดพลาดกำลังสอง;
- ขั้นต่ำของสัมประสิทธิ์ Gini;
การรู้จักปัจจัยที่เหมาะสมสามารถมีประโยชน์ในการ:
- ปรับค่าข้อมูลนำเข้า (การเปลี่ยนแปลงราคา) สำหรับเครือข่ายประสาทและอัลกอริธึมการเรียนรู้ของเครื่องอื่นๆ;
- ประเมินจำนวนแท่งที่เพียงพอสำหรับการสุ่มเป็นเวกเตอร์นำเข้าสำหรับการวิเคราะห์ในระบบการเทรดความผันผวน;
- ตรวจจับสัญลักษณ์และ/หรือกรอบเวลา (timeframes) ที่มีความผิดปกติ (F ที่ไม่สม่ำเสมอหรือความเป็นเอกลักษณ์ในกราฟการกระจาย);
Input
- Period — ระยะห่างสูงสุดในแท่ง (N) ที่จะใช้ในการเก็บสถิติการเปลี่ยนแปลงราคา โดยค่าเริ่มต้นคือ 200;
- Factor — ยกกำลังสำหรับ "การเฉลี่ย" ตามระยะห่าง โดยค่าเริ่มต้นคือ 0 - หมายถึงการตรวจจับอัตโนมัติ สามารถป้อนค่าที่กำหนดเองระหว่าง 0.0 ถึง 1.0 สำหรับการประมาณ เช่น 0.525;
- Method — หนึ่งในวิธีการประเมินความสม่ำเสมอ: ความแปรปรวน, triple_M, Gini;
- MaxBars — ขีดจำกัดของแท่งในการคำนวณสถิติ โดยค่าเริ่มต้นคือ 0 - หมายถึงแท่งทั้งหมดที่มี;
หมายเหตุ: หากคุณใช้จำนวนแท่งที่ไม่จำกัดหรือหลายแสนแท่งในกราฟ การคำนวณอาจใช้เวลานาน—หากนี่เป็นปัญหา ควรพิจารณาจำกัดจำนวนแท่งให้เป็นหลักหมื่น
Output
ตัวชี้วัดจะแสดงฮิสโตแกรมสีฟ้าของการเปลี่ยนแปลงราคาที่เฉลี่ยต่อแท่งสำหรับแต่ละระยะห่างในช่วงของระยะห่าง (1..Period) และสำหรับปัจจัยความสม่ำเสมอที่เลือก
นอกจากนี้ยังมีการแสดงจำนวนแท่ง (ระยะห่าง) ที่เพิ่มขึ้นอย่างต่อเนื่องในฮิสโตแกรมที่สอง (สีส้ม) เพื่อใช้เป็นข้อมูลอ้างอิง
ตารางที่สมบูรณ์ของปัจจัยที่ทดสอบและเมตริกที่เกี่ยวข้องของลำดับเวลาปัจจุบันจะถูกพิมพ์ในบันทึก
ภาพหน้าจอ
ภาพหน้าจอด้านล่างนี้แสดงตัวชี้วัดใน 3 เฟรมเวลา: D1, H1, M1
แต่ละกราฟมีตัวชี้วัด 2 ตัว:
- ตัวบนถูกตั้งค่าให้ตรวจจับ F โดย Gini โดยค่าที่พบ (เปลี่ยนแปลงระหว่าง 0.4 หนึ่งครั้ง และ 0.5 สองครั้ง) แสดงในชื่อ และทำเครื่องหมายด้วยดอกจัน;
- ตัวล่างถูกตั้งค่าที่ F=0.6;
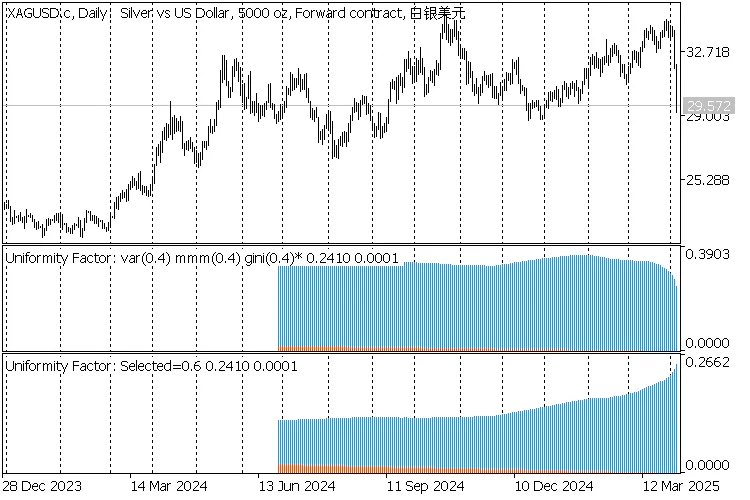
2 indicators Uniformity Factor on XAGUSD,D1
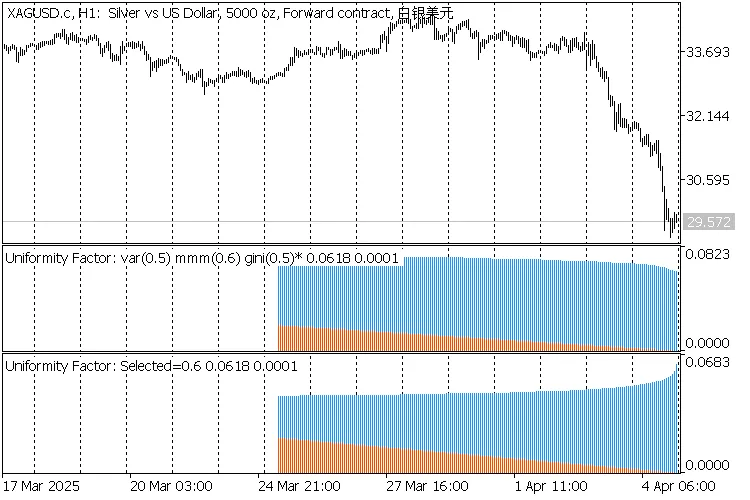
2 indicators Uniformity Factor on XAGUSD,H1
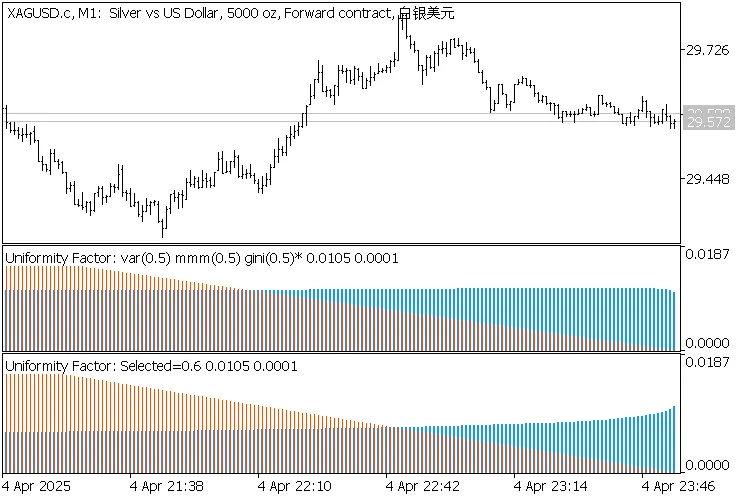
2 indicators Uniformity Factor on XAGUSD,M1
โพสต์ที่เกี่ยวข้อง
- เครื่องมือ Open Range Breakout สำหรับ MetaTrader 5
- เครื่องมือ Master Tools - อินดิเคเตอร์สำหรับ MetaTrader 4
- Condition Scanner: เครื่องมือวิเคราะห์อัตโนมัติสำหรับ MetaTrader 4
- FX Multi-Meter II: เครื่องมือช่วยเทรดที่ครบครันสำหรับนักลงทุน
- เครื่องมือ MetaCOT 2 CFTC ToolBox - ชุดตัวชี้วัดสำหรับการวิเคราะห์ใน MetaTrader 4