Einleitung
Es gibt zahlreiche Programme, die die Erstellung von selbstähnlichen Mengen ermöglichen, definiert durch Iterierte Funktionensysteme (IFS). Beispiele hierfür sind Fractint, Fractal Designer oder IFS Matlab Generator. Dank der Geschwindigkeit der MQL5-Sprache und der Möglichkeit, mit grafischen Objekten zu arbeiten, können diese schönen Mengen im MetaTrader 5 Clientterminal untersucht werden.
Die cIntBMP Bibliothek, entwickelt von Dmitry (Integer), bietet neue grafische Möglichkeiten und vereinfacht erheblich die Erstellung von grafischen Bildern. Diese Bibliothek wurde mit einem Sonderpreis ausgezeichnet von MetaQuotes Software Corp.
In diesem Beitrag betrachten wir Beispiele zur Arbeit mit der cIntBMP-Bibliothek. Zudem werden wir die Algorithmen zur Erstellung von Fraktalmengen unter Verwendung der Iterierten Funktionensysteme behandeln.
1. Affine Transformation der Ebene
Die affine Transformation der Ebene ist eine Abbildung, die durch eine Matrix und einen Vektor definiert wird. Ein Punkt mit den Koordinaten (x,y) wird durch eine lineare Transformation in einen anderen Punkt transformiert:
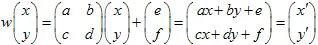
Die Transformation muss nicht-singulär sein, der Determinant muss ungleich null sein. Die affine Transformation ändert die Größe um den Faktor des Determinanten.
Affine Transformationen verändern nicht die Struktur geometrischer Objekte (die Linien bleiben Linien). Sie ermöglichen einfache "Verformungen" der Objekte, wie Rotation, Skalierung und Translation.
Beispiele für affine Ebene-Transformationen:
1) Rotation der Ebene um einen Winkel:
2) Skalierung der Ebene mit den Koeffizienten (X und Y Achse):
3) Translation der Ebene durch einen Vektor:
Die Kontraktionsabbildungen sind der Schlüssel (siehe Hutchinson Ergebnisse).
Wenn zwei Punkte Koordinaten haben, so ist die affine Transformation eine Kontraktion, wenn die Bedingungen erfüllt sind.
Hier ist ein Beispiel für eine affine Transformation:

Das Ergebnis ist:
2. Ähnlichkeits-Transformationen
Fraktale werden auf folgende Weise konstruiert: Ein geometrisches Objekt (Abschnitt, Dreieck, Quadrat) wird in N Teile unterteilt und M davon werden für den weiteren "Aufbau" der Menge verwendet (wenn N=M, erhalten wir die ganzzahlige Dimension der resultierenden Menge). Dieser Prozess wird fortlaufend für jedes der Teile wiederholt.
Beispiele klassischer Fraktale:
- Triadische Koch-Kurve, N=3, M=4;
- Cantor-Staub, N=3, M=2;
Dreieck:
- Sierpinski-Teppich, N=4, M=3;
Quadrate:
- Sierpinski-Teppich, N=9, M=8;
- Vichek-Fraktal, N=9, M=5.
usw.
Die Fraktale haben eine selbstähnliche Struktur und können durch mehrere Ähnlichkeitstransformationen definiert werden. Die Struktur der affinen Transformation hängt von der Art der Fraktalkonstruktion ab.
Wie Sie weiter sehen werden, ist es ganz einfach, und das einzige Problem, das wir lösen müssen, ist die Beschreibung der ersten Iteration der Fraktalkonstruktion und die Findung der entsprechenden Menge an affinen Transformationen.
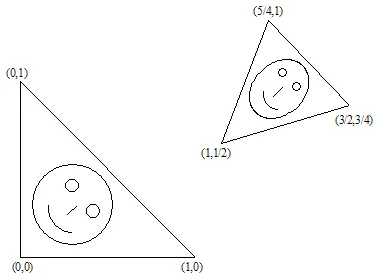
Angenommen, wir haben eine Menge. Nach dem Algorithmus zur Fraktalerstellung müssen wir sie reduzieren, rotieren und an einen bestimmten Ort setzen. Das Problem besteht darin, diesen Prozess mithilfe affiner Transformationen zu beschreiben, d.h. wir müssen die Matrix und den Vektor finden.
Es ist leicht zu beweisen, dass es ausreicht, 3 Punkte der ursprünglichen Menge (nichttrivial) zu nehmen und sie in 3 entsprechende Punkte der "reduzierten" Menge zu transformieren. Diese Transformation führt zu 6 linearen Gleichungen, die es uns ermöglichen, die a, b, c, d, e und f als Lösung zu finden.
Lassen Sie uns das zeigen. Angenommen, ein Dreieck wird in ein anderes Dreieck transformiert.
Durch Lösen des Systems linearer Gleichungen können wir die Koeffizienten a, b, c, d, e und f erhalten:
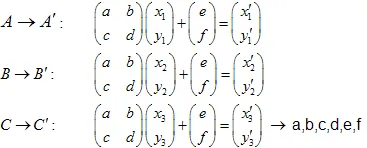
Beispiel: Sierpinski-Teppich:
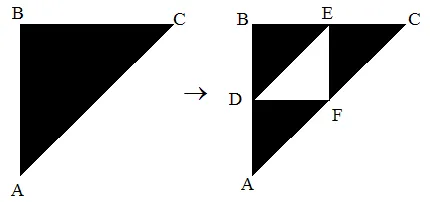
Die Koordinaten der Punkte sind:
- A (0,0)
- B (0,1)
- C (1,1)
- D (0,1/2)
- E (1/2,1)
- F (1/2,1/2)
Wir haben 3 Transformationen:
- ABC -> ADF
- ABC -> DBE
- ABC -> FEC
Das System der linearen Gleichungen sieht wie folgt aus:
Die Lösungen sind:  ,
, 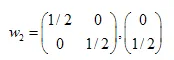 ,
, 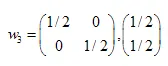
Wir haben die Koeffizienten der drei affinen Transformationen gefunden. Diese werden wir für die Erstellung selbstähnlicher Mengen verwenden.
3. Fraktale mit Iterierten Funktionensystemen erstellen
Das Iterierte Funktionensystem (IFS) ist eine Menge von affinen Kontraktionen, wobei jede IFS-Funktion durch 7 Zahlen definiert ist. Die Gewichtungen, die für den Iterationsprozess verwendet werden, sind proportional zur Kontraktion.
Betrachten wir den Algorithmus zur Fraktalerstellung unter Verwendung des Iterierten Funktionensystems.
Zunächst nehmen wir einen Ausgangspunkt mit Koordinaten. Dann wählen wir zufällig einige der Kontraktionen aus und zeichnen den Punkt. Wiederholen wir diesen Vorgang für eine große Anzahl an Punkten, werden wir die Struktur des Fraktals sehen, trotz des zufälligen Prozesses.
Hier ist ein Beispiel des Sierpinski-Teppichs:
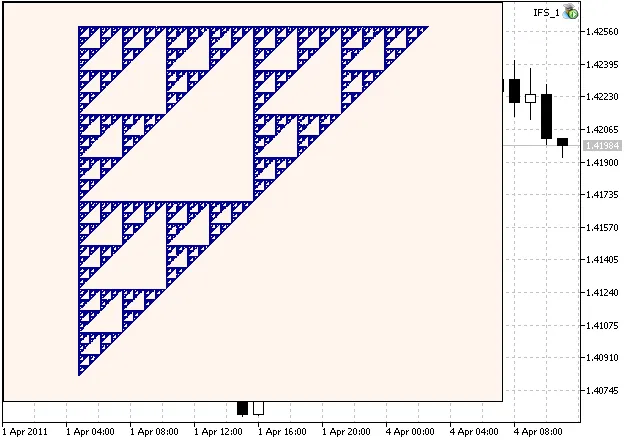
Abbildung 1. Der Sierpinski-Teppich, generiert mit IFS-Koeffizienten aus Kapitel 2
Der Code:
//+------------------------------------------------------------------+ //| IFS_Sierpinski_Gasket.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" //-- include file with cIntBMP class #include <cIntBMP.mqh> //-- Sierpinski Gasket IFS coefficients //-- (a,b,c,d) matrices double IFS_a[3] = {0.50, 0.50, 0.50}; double IFS_b[3] = {0.00, 0.00, 0.00}; double IFS_c[3] = {0.00, 0.00, 0.00}; double IFS_d[3] = {0.50, 0.50, 0.50}; //-- (e,f) vectors double IFS_e[3] = {0.00, 0.00, 0.50}; double IFS_f[3] = {0.00, 0.50, 0.50}; //-- "probabilities" of transforms, multiplied by 1000 double IFS_p[3]={333,333,333}; double Probs[3]; // Probs array - used to choose IFS transforms cIntBMP bmp; // cIntBMP class instance int scale=350; // scale coefficient //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //-- Prepare Probs array double m=0; for(int i=0; i<ArraySize(IFS_p); i++) { Probs[i]=IFS_p[i]+m; m=m+IFS_p[i]; } //-- size of BMP image int XSize=500; int YSize=400; //-- create bmp image XSizexYSize with clrSeashell background color bmp.Create(XSize,YSize,clrSeashell); //-- image rectangle bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack); //-- point coordinates (will be used in construction of set) double x0=0; double y0=0; double x,y; //-- number of points to calculate (more points - detailed image) int points=1500000; //-- calculate set for(int i=0; i<points; i++) { // choose IFS tranform with probabilities, proportional to defined double prb=1000*(rand()/32767.0); for(int k=0; k<ArraySize(IFS_p); k++) { if(prb<=Probs[k]) { // affine transformation x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k]; y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k]; // update previous coordinates x0 = x; y0 = y; // convert to BMP image coordinates // (note the Y axis in cIntBMP) int scX = int (MathRound(XSize/2 + (x-0.5)*scale)); int scY = int (MathRound(YSize/2 + (y-0.5)*scale)); // if the point coordinates inside the image, draw the dot if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrDarkBlue); } break; } } } //-- save image to file bmp.Save("bmpimg",true); //-- plot image on the chart bmp.Show(0,0,"bmpimg","IFS"); //--- return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- delete image from the chart ObjectDelete(0,"IFS"); //--- delete file bmp.Delete("bmpimg",true); } //+------------------------------------------------------------------+
Wenn wir die Skalierung auf 1350 setzen, die Anzahl der Iterationen auf 15000000 erhöhen und den Ausgangspunkt verschieben, können wir einen vergrößerten Bereich der Menge sehen.
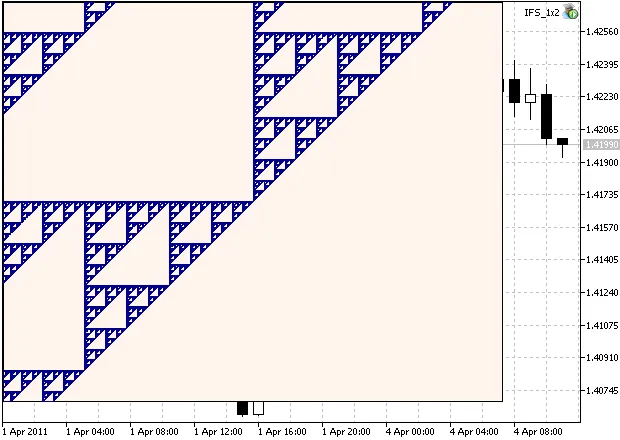
Abbildung 2. Vergrößerter Bereich des Sierpinski-Teppichs
Lassen Sie uns das berühmte Barnsleys Farn betrachten, das von Michael Barnsley vorgeschlagen wurde. Es ist komplexer.

Abbildung 3. Barnsleys Farn
Der Code ist ähnlich, aber in diesem Fall haben wir 4 IFS-Kontraktionen mit unterschiedlichen Gewichten.
//+------------------------------------------------------------------+ //| IFS_fern.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #include <cIntBMP.mqh> //-- Barnsley Fern IFS coefficients //-- (a,b,c,d) matrices double IFS_a[4] = {0.00, 0.85, 0.20, -0.15}; double IFS_b[4] = {0.00, 0.04, -0.26, 0.28}; double IFS_c[4] = {0.00, -0.04, 0.23, 0.26}; double IFS_d[4] = {0.16, 0.85, 0.22, 0.24}; //-- (e,f) vectors double IFS_e[4] = {0.00, 0.00, 0.00, 0.00}; double IFS_f[4] = {0.00, 1.60, 1.60, 0.00}; //--

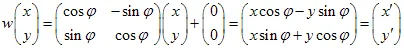
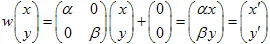
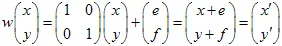
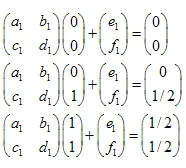

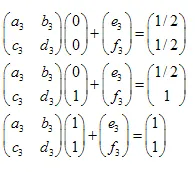
Kommentar 0