指标设置
要设置斐波那契锯齿指标,我们需要:
- 1 个锯齿图形
- 2 个数据缓冲区用于存储高点和低点
- 输入参数
- 一组系统变量,指标重新计算时会重置
代码示例:
#property indicator_buffers 2 #property indicator_plots 1 input double retracement=23.6; //回撤比例 input double minSizeInAtrUnits=0.0; //波动最小尺寸 input int rollingAtrPeriod=14; //滚动 ATR 周期 input color Color=clrDodgerBlue; //波动颜色 input int Width=3; //波动宽度 input ENUM_LINE_STYLE Style=STYLE_SOLID; //波动样式 //--- 上升波动和下降波动 double upWaves[], dwWaves[];
upWaves 数组将存储高点,dwWaves 数组将存储低点。
系统变量:
我们需要跟踪最后的波动类型、开始和结束位置、起始和结束的柱数距离。
另外,我们还需要本地高点和低点变量,以及每个点的柱数距离。
//--- 记录锯齿波动状态 int wave_type=0; //波动类型 [0] 无 [1] 上升 [2] 下降 double wave_start_price=0.0; //波动开始价格 double wave_end_price=0.0; //波动结束价格 int wave_start_distance=0; //开始价格到当前的柱数距离 int wave_end_distance=0; //结束价格到当前的柱数距离 double high_mem=0.0; //高点跟踪 int distance_from_high=0; //距离高点的柱数 double low_mem=0.0; //低点跟踪 int distance_from_low=0; //距离低点的柱数 double rollingAtr=0.0; //滚动 ATR int rollingAtrs=0; //已计算的滚动 ATR
最后,我们需要定义一个系统重置函数:
void resetSystem(){
ArrayFill(upWaves,0,ArraySize(upWaves),0.0);
ArrayFill(dwWaves,0,ArraySize(dwWaves),0.0);
wave_type=0;
wave_start_price=0.0;
wave_end_price=0.0;
wave_start_distance=0;
wave_end_distance=0;
high_mem=0.0;
low_mem=0.0;
distance_from_high=0;
distance_from_low=0;
rollingAtr=0.0;
rollingAtrs=0;
} 标准操作,填充数组为零并重置系统变量。
在初始化时,我们设置缓冲区、绘图并第一次调用重置函数:
SetIndexBuffer(0, upWaves, INDICATOR_DATA); SetIndexBuffer(1, dwWaves, INDICATOR_DATA); PlotIndexSetDouble(0, PLOT_EMPTY_VALUE, 0.0); PlotIndexSetInteger(0, PLOT_DRAW_TYPE, DRAW_ZIGZAG); PlotIndexSetInteger(0, PLOT_LINE_COLOR, 0, Color); PlotIndexSetInteger(0, PLOT_LINE_WIDTH, Width); PlotIndexSetInteger(0, PLOT_LINE_STYLE, Style); resetSystem();
现在让我们深入计算部分。
首先,我们需要处理滚动 ATR。
在收集的柱数未超过 ATR 周期之前,我们不会进行其他操作。
管理滚动 ATR 的代码如下:
- 如果未收集超过周期的柱数,则继续将找到的柱数范围添加到总和中
- 一旦达到周期,进行第一次除法(平均)
- 之后,减去滚动 ATR 的一部分,并添加新的一部分
我们将最后一部分放在前面,因为它会更频繁地发生,避免访问两个 if 语句。
代码如下:
//--- 管理 ATR
rollingAtrs++;
if(rollingAtrs>rollingAtrPeriod){
double new_portion=((high[i]-low[i])/_Point)/((double)rollingAtrPeriod);
rollingAtr=(rollingAtr)-(rollingAtr/((double)rollingAtrPeriod))+new_portion;
}
else if(rollingAtrs<=rollingAtrPeriod){
rollingAtr+=(high[i]-low[i])/_Point;
if(rollingAtrs==rollingAtrPeriod){
rollingAtr/=((double)rollingAtrs);
high_mem=high[i];
low_mem=low[i];
distance_from_high=0;
distance_from_low=0;
}
} 接下来,我们需要处理的是回撤的问题。
为了能够进行回撤,必须至少有一个波动。
但第一波会回撤什么呢?:D
为此,我们将进行如下处理:
- 一旦 ATR 滿足(ATR 收集 = 周期),我们将抓取系统变量中的高点和低点
- 无论哪个方向形成的波动满足有效尺寸并且形成新的高点(上升波)或新的低点(下降波),我们就以此为胜
这样我们就能开始波动序列,而不需要用回撤来作为初始波动。
注意,我们也可以选择在这里采用经典的分形方法来处理第一波,然后继续使用回撤。
以下是当我们还没有波动类型时的处理代码:
else{
//--- 如果突破高点而未突破低点
if(high[i]>high_mem&&low[i]>=low_mem){
double new_wave_size_in_atr_units=((high[i]-low_mem)/_Point)/rollingAtr;
if(new_wave_size_in_atr_units>=minSizeInAtrUnits){
wave_type=1;
wave_start_price=low_mem;
wave_start_distance=distance_from_low;
wave_end_price=high[i];
wave_end_distance=0;
dwWaves[i-wave_start_distance]=low_mem;
upWaves[i]=high[i];
high_mem=high[i];
distance_from_high=0;
low_mem=low[i];
distance_from_low=0;
}
}
//--- 如果突破低点而未突破高点
else if(low[i]<low_mem&&high[i]<=high_mem){
double new_wave_size_in_atr_units=((high_mem-low[i])/_Point)/rollingAtr;
if(new_wave_size_in_atr_units>=minSizeInAtrUnits){
wave_type=-1;
wave_start_price=high_mem;
wave_start_distance=distance_from_high;
wave_end_price=low[i];
wave_end_distance=0;
upWaves[i-wave_start_distance]=high_mem;
dwWaves[i]=low[i];
high_mem=high[i];
distance_from_high=0;
low_mem=low[i];
distance_from_low=0;
}
}
//--- 如果突破高低点
else if(low[i]<low_mem&&high[i]>high_mem){
high_mem=high[i];
low_mem=low[i];
distance_from_high=0;
distance_from_low=0;
}
} 非常好,最后一块内容。
- 如果我们有上升波:
- 如果产生新高,则将锯齿线从之前的高点位置移动到新高点,并更新低点和低点的距离。
- 如果产生新低,或设定新的低点,则计算从高点到低点的距离并将其除以波动大小,并乘以 100 以匹配输入参数规模。
相关代码如下:
if(wave_type==1){
//--- 如果波动向上扩展
if(high[i]>wave_end_price){
upWaves[i-wave_end_distance]=0.0;
upWaves[i]=high[i];
wave_end_price=high[i];
wave_end_distance=0;
high_mem=high[i];
distance_from_high=0;
low_mem=low[i];
distance_from_low=0;
}
//--- 检查回撤
if(low[i]<low_mem||distance_from_low==0){
low_mem=low[i];
distance_from_low=0;
double size_of_wave=(wave_end_price-wave_start_price)/_Point;
double size_of_retracement=(wave_end_price-low_mem)/_Point;
if(size_of_wave>0.0){
double retraced=(size_of_retracement/size_of_wave)*100.0;
double new_wave_size_in_atr_units=((wave_end_price-low_mem)/_Point)/rollingAtr;
if(new_wave_size_in_atr_units>=minSizeInAtrUnits){
if(retraced>=retracement){
wave_type=-1;
wave_start_price=high[i-distance_from_high];
wave_start_distance=distance_from_high;
wave_end_price=low[i];
wave_end_distance=0;
upWaves[i-wave_start_distance]=high_mem;
dwWaves[i]=low[i];
high_mem=high[i];
distance_from_high=0;
low_mem=low[i];
distance_from_low=0;
}
}
}
} 当我们有下降波时,处理方法是反的。
至此,我们的回撤锯齿指标就完成了。
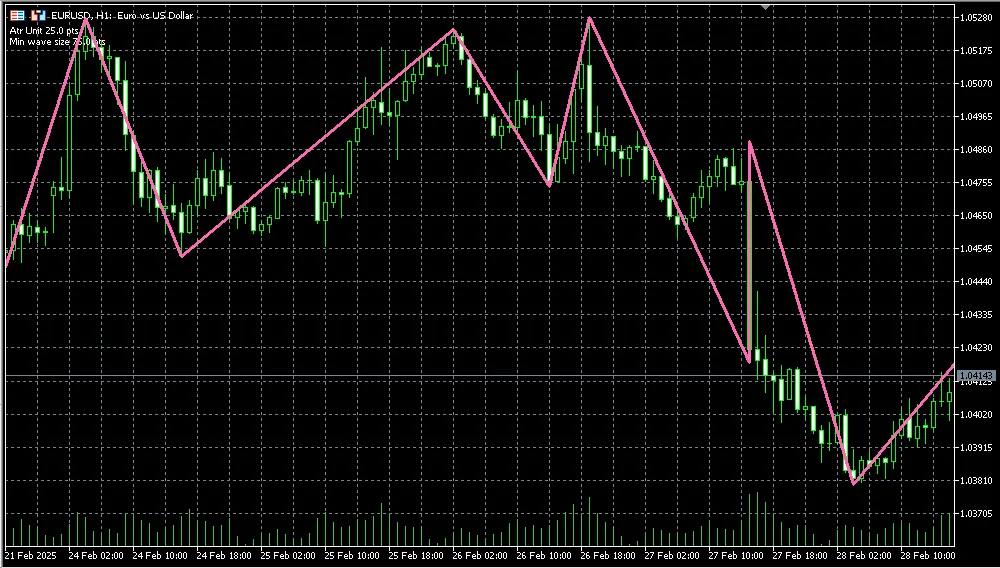
下面是回撤比例为 23.6% 和波动最小尺寸为 0.0 的锯齿图:

而这是同样的锯齿图,波动最小尺寸为 3:

评论 0