Introducción
Hoy vamos a hablar sobre cómo crear conjuntos auto-similares utilizando el sistema de funciones iteradas (IFS) en MQL5. Existen varios programas que facilitan esta tarea, como IFS. Algunos ejemplos conocidos son Fractint y Fractal Designer. Gracias a la rapidez del lenguaje MQL5 y su capacidad para trabajar con objetos gráficos, podemos estudiar estos conjuntos fascinantes en el terminal cliente de MetaTrader 5.
La biblioteca cIntBMP, desarrollada por Dmitry (Integer), ofrece nuevas oportunidades gráficas y simplifica enormemente la creación de imágenes gráficas. Esta biblioteca fue premiada con un premio especial por MetaQuotes Software Corp.
En esta publicación, exploraremos ejemplos de cómo trabajar con la biblioteca cIntBMP. Además, cubriremos los algoritmos de creación de conjuntos fractales utilizando sistemas de funciones iteradas.
1. Transformación Afín del Plano
La transformación afín del plano es una representación que se puede visualizar de la siguiente manera: 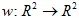 . Generalmente, la transformación afín 2D se puede definir con una matriz
. Generalmente, la transformación afín 2D se puede definir con una matriz 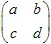 y un vector
y un vector 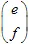 . El punto con coordenadas (x,y) se transforma a otro punto
. El punto con coordenadas (x,y) se transforma a otro punto 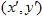 utilizando la transformación lineal:
utilizando la transformación lineal:
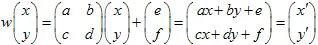
La transformación debe ser no singular, es decir, 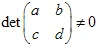 . La transformación afín cambia el tamaño
. La transformación afín cambia el tamaño 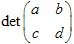 veces.
veces.
Las transformaciones afines no cambian la estructura de los objetos geométricos (las líneas se transforman en líneas). Esto permite describir deformaciones simples de los objetos, como rotación, escalado y traslación.
Ejemplos de transformaciones afines del plano:
1) Rotación del plano en un ángulo:
2) Escalado del plano con coeficientes
y
(ejes X e Y):
3) Traslación del plano por un vector
:
Las mappings de contracción son clave (ver resultados de Hutchinson).
Si 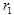 y
y 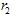 tienen coordenadas
tienen coordenadas 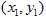 y
y 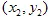 y
y 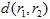 es una métrica (por ejemplo, métrica euclidiana:
es una métrica (por ejemplo, métrica euclidiana: 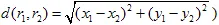 ). La transformación afín se llama contracción si
). La transformación afín se llama contracción si 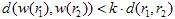 , donde
, donde 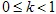 .
.
Aquí hay un ejemplo de transformación afín:

El resultado es:
2. Transformaciones de Similitud
Los fractales se construyen de la siguiente manera: algún objeto geométrico simple (sección, triángulo, cuadrado) se divide en N piezas y M de ellas se utilizan para la "construcción" posterior del conjunto (si N=M, obtendremos la dimensión entera del conjunto resultante). Este proceso se repite una y otra vez para cada una de las piezas.
Fractales clásicos:
Secciones:
- Curva de Koch, N=3, M=4;
- Polvo de Cantor, N=3, M=2;
Triángulo:
- Gasket de Sierpinski, N=4, M=3;
Cuadrados:
- Alfombra de Sierpinski, N=9, M=8;
- Fractal de Vichek, N=9, M=5.
y así sucesivamente.
Los fractales tienen una estructura auto-similar, algunos de ellos pueden definirse mediante varias transformaciones de similitud. La estructura de la transformación afín depende de la forma en que se construye el fractal.
Como verás más adelante, es muy simple, y el único problema que tenemos que resolver es describir solo la primera iteración de la construcción del fractal y encontrar el conjunto correspondiente de transformaciones afines.
Supongamos que tenemos un conjunto. Según el algoritmo de creación del fractal, necesitamos reducirlo, rotarlo y "colocarlo en un lugar determinado". El problema es describir este proceso utilizando transformaciones afines, es decir, necesitamos encontrar la matriz y el vector.
Es fácil demostrar que es suficiente tomar 3 puntos del conjunto inicial (no triviales) y transformarlos en 3 puntos correspondientes del conjunto "reducido". Esta transformación conducirá a 6 ecuaciones lineales, que nos permitirán encontrar los coeficientes a,b,c,d,e,f como solución.
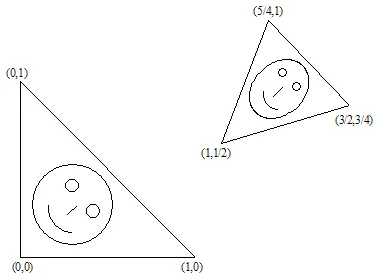
Mostremos un ejemplo. Supongamos que el triángulo 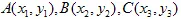 se transforma en el triángulo
se transforma en el triángulo 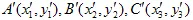 .
.
Al resolver el sistema de ecuaciones lineales, podremos obtener los coeficientes a,b,c,d,e y f:
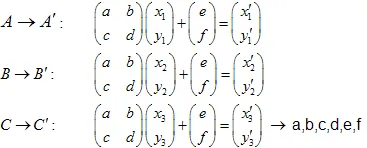
Ejemplo: Gasket de Sierpinski:
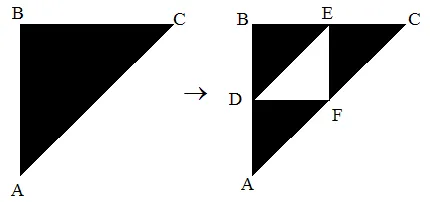
Las coordenadas de los puntos son:
- A (0,0)
- B (0,1)
- C (1,1)
- D(0,1/2)
- E (1/2,1)
- F(1/2,1/2)
Tenemos 3 transformaciones:
- ABC -> ADF
- ABC -> DBE
- ABC -> FEC
El sistema de ecuaciones lineales se ve así:
Las soluciones son:  ,
, 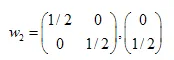 ,
, 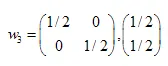
Hemos encontrado los coeficientes de tres transformaciones afines. A partir de aquí, los utilizaremos para crear conjuntos auto-similares.
3. Creando Fractales Usando los Sistemas de Funciones Iteradas
El Sistema de Funciones Iteradas (IFS) es un conjunto de contracciones afines 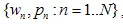 donde
donde 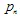 - son los "pesos". Cada una de las funciones de IFS está definida por 7 números:
- son los "pesos". Cada una de las funciones de IFS está definida por 7 números: 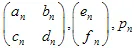 , donde
, donde 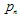 los pesos se utilizan durante el proceso de iteración como probabilidad de la n-ésima transformación. Es mejor definir sus valores, proporcional a la contracción:
los pesos se utilizan durante el proceso de iteración como probabilidad de la n-ésima transformación. Es mejor definir sus valores, proporcional a la contracción: 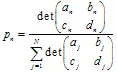 .
.
Consideremos el algoritmo de construcción de fractales utilizando el Sistema de Funciones Iteradas (ver también Juego del Caos).
Primero necesitamos tomar un punto inicial con coordenadas 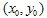 . Luego, elegimos aleatoriamente algunas de las contracciones y trazamos el punto
. Luego, elegimos aleatoriamente algunas de las contracciones y trazamos el punto 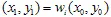 . Y otra vez, elegimos aleatoriamente una de las contracciones
. Y otra vez, elegimos aleatoriamente una de las contracciones 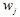 y trazamos
y trazamos 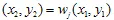 . Finalmente, tendremos el
. Finalmente, tendremos el 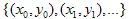 como un conjunto de puntos.
como un conjunto de puntos.
La elección de contracción depende de su "probabilidad". Si repetimos el proceso (por ejemplo, ~30000 puntos) y trazamos el conjunto resultante, veremos su estructura a pesar del proceso aleatorio.
Aquí hay un ejemplo del Gasket de Sierpinski:
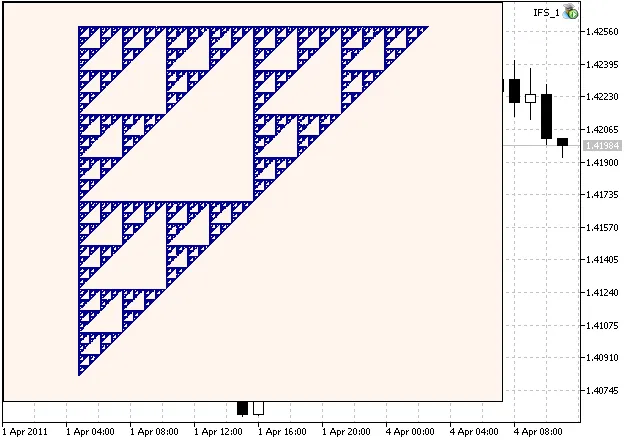
Figura 1. El Gasket de Sierpinski, generado con coeficientes IFS calculados en el capítulo 2
El código:
//+------------------------------------------------------------------+ //| IFS_Sierpinski_Gasket.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" //-- include file with cIntBMP class #include <cIntBMP.mqh> //-- Sierpinski Gasket IFS coefficients //-- (a,b,c,d) matricies double IFS_a[3] = {0.50, 0.50, 0.50}; double IFS_b[3] = {0.00, 0.00, 0.00}; double IFS_c[3] = {0.00, 0.00, 0.00}; double IFS_d[3] = {0.50, 0.50, 0.50}; //-- (e,f) vectors double IFS_e[3] = {0.00, 0.00, 0.50}; double IFS_f[3] = {0.00, 0.50, 0.50}; //-- "probabilities" of transforms, multiplied by 1000 double IFS_p[3]={333,333,333}; double Probs[3]; // Probs array - used to choose IFS transforms cIntBMP bmp; // cIntBMP class instance int scale=350; // scale coefficient //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //-- Prepare Probs array double m=0; for(int i=0; i<ArraySize(IFS_p); i++) { Probs[i]=IFS_p[i]+m; m=m+IFS_p[i]; } //-- size of BMP image int XSize=500; int YSize=400; //-- create bmp image XSizexYSize with clrSeashell background color bmp.Create(XSize,YSize,clrSeashell); //-- image rectangle bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack); //-- point coordinates (will be used in construction of set) double x0=0; double y0=0; double x,y; //-- number of points to calculate (more points - detailed image) int points=1500000; //-- calculate set for(int i=0; i<points; i++) { // choose IFS tranform with probabilities, proportional to defined double prb=1000*(rand()/32767.0); for(int k=0; k<ArraySize(IFS_p); k++) { if(prb<=Probs[k]) { // affine transformation x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k]; y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k]; // update previous coordinates x0 = x; y0 = y; // convert to BMP image coordinates // (note the Y axis in cIntBMP) int scX = int (MathRound(XSize/2 + (x-0.5)*scale)); int scY = int (MathRound(YSize/2 + (y-0.5)*scale)); // if the point coordinates inside the image, draw the dot if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrDarkBlue); } break; } } } //-- save image to file bmp.Save("bmpimg",true); //-- plot image on the chart bmp.Show(0,0,"bmpimg","IFS"); //--- return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- delete image from the chart ObjectDelete(0,"IFS"); //--- delete file bmp.Delete("bmpimg",true); } //+------------------------------------------------------------------+
Si configuramos la escala a 1350, aumentamos el número de iteraciones a 15000000 y cambiamos el desplazamiento del punto inicial:
int scX = MathRound(XSize/2 + (x-0.75)*scale); int scY = MathRound(YSize/2 + (y-0.75)*scale);
podremos ver la región ampliada del conjunto. Se puede observar (Fig. 2) que tiene una estructura auto-similar:
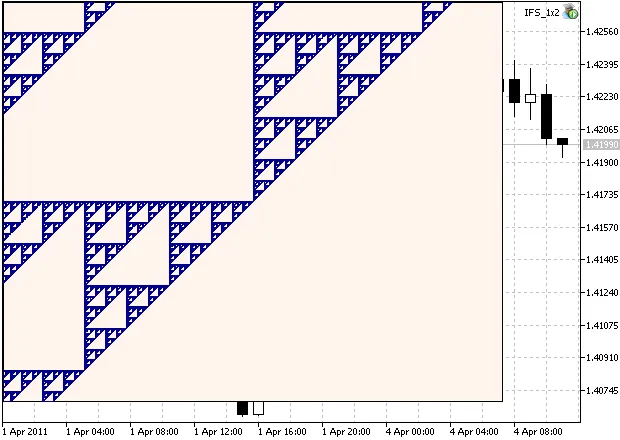
Figura 2. Región ampliada del Gasket de Sierpinski
Consideremos el famoso Feto de Barnsley, propuesto por Michael Barnsley. Es más complejo.

Figura 3. Feto de Barnsley
El código es similar, pero en este caso tenemos 4 contracciones de IFS con diferentes pesos.
//+------------------------------------------------------------------+ //| IFS_fern.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #include <cIntBMP.mqh> //-- Barnsley Fern IFS coefficients //-- (a,b,c,d) matricies double IFS_a[4] = {0.00, 0.85, 0.20, -0.15}; double IFS_b[4] = {0.00, 0.04, -0.26, 0.28}; double IFS_c[4] = {0.00, -0.04, 0.23, 0.26}; double IFS_d[4] = {0.16, 0.85, 0.22, 0.24}; //-- (e,f) vectors double IFS_e[4] = {0.00, 0.00, 0.00, 0.00}; double IFS_f[4] = {0.00, 1.60, 1.60, 0.00}; //-- "probabilities" of transforms, multiplied by 1000 double IFS_p[4] = {10, 850, 70, 70}; double Probs[4]; cIntBMP bmp; int scale=50; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { double m=0; for(int i=0; i<ArraySize(IFS_p); i++) { Probs[i]=IFS_p[i]+m; m=m+IFS_p[i]; } int XSize=600; int YSize=600; bmp.Create(XSize,YSize,clrSeashell); bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack); double x0=0; double y0=0; double x,y; int points=250000; for(int i=0; i<points; i++) { double prb=1000*(rand()/32767.0); for(int k=0; k<ArraySize(IFS_p); k++) { if(prb<=Probs[k]) { x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k]; y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k]; x0 = x; y0 = y; int scX = int (MathRound(XSize/2 + (x)*scale)); int scY = int (MathRound(YSize/2 + (y-5)*scale)); if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrForestGreen); } break; } } } bmp.Save("bmpimg",true); bmp.Show(0,0,"bmpimg","IFS"); //--- return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- delete image from the chart ObjectDelete(0,"IFS"); //--- delete file bmp.Delete("bmpimg",true); } //+------------------------------------------------------------------+
Es notable que tal estructura compleja puede definirse con solo 28 números.
Si aumentamos la escala a 150, y establecemos las iteraciones a 1250000, veremos el fragmento ampliado:
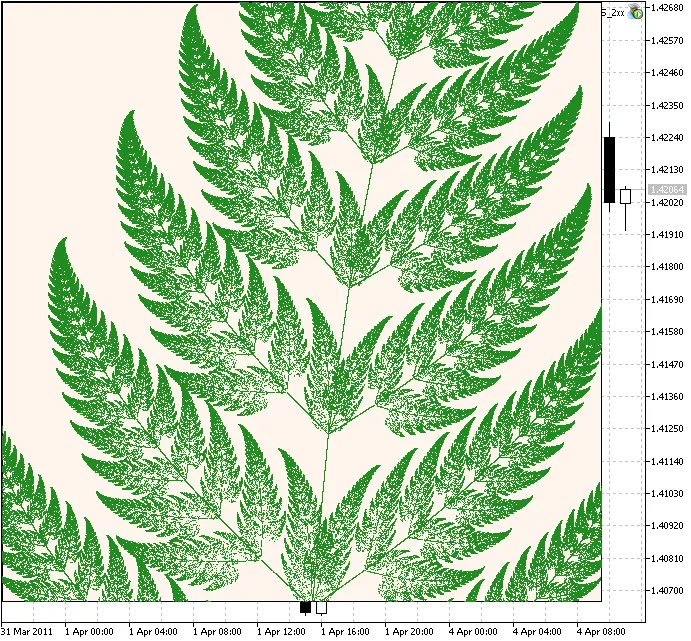
Figura 4. Un fragmento del Feto de Barnsley
Como verás, el algoritmo es universal; permite generar diferentes conjuntos fractales.
El siguiente ejemplo es la Alfombra de Sierpinski, definida por los siguientes coeficientes de IFS:
//-- Sierpinski Gasket IFS coefficients double IFS_a[8] = {0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333}; double IFS_b[8] = {0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00}; double IFS_c[8] = {0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00}; double IFS_d[8] = {0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333}; double IFS_e[8] = {-0.125, -3.375, -3.375, 3.125, 3.125, -3.375, -0.125, 3.125}; double IFS_f[8] = {6.75, 0.25, 6.75, 0.25, 6.75, 3.5, 0.25, 3.50}; //-- "probabilities", multiplied by 1000 double IFS_p[8]={125,125,125,125,125,125,125,125};
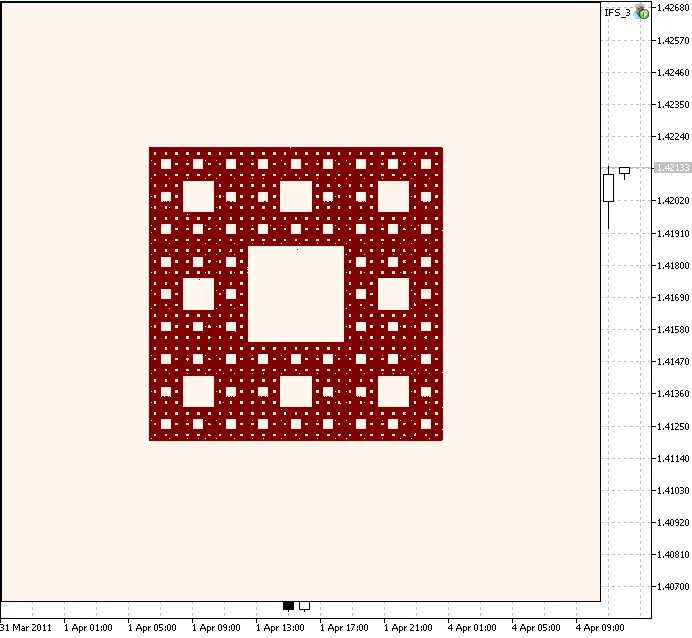
Figura 5. Alfombra de Sierpinski
En el capítulo 2 hemos considerado el algoritmo de cálculo de coeficientes de contracciones de IFS.
Ahora, exploremos cómo crear las "palabras fractales". En ruso, la palabra "Fractales" se ve así:
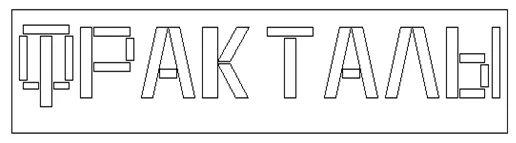
Figura 6. La palabra "Fractales" en ruso
Para encontrar los coeficientes de IFS, necesitamos resolver los sistemas lineales correspondientes. Las soluciones son:
//-- IFS coefficients of the 
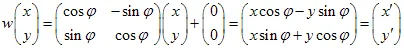
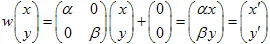
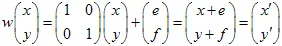
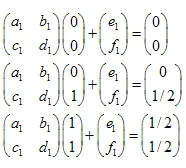

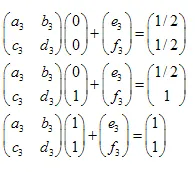
Comentarios 0