소개
자기 유사 집합을 생성할 수 있는 다양한 프로그램들이 있습니다. 이들은 반복 함수 시스템(IFS)에 기반하고 있습니다. 예를 들어, 프랙틴트, 프랙탈 디자이너 등이 있습니다. MQL5 언어의 빠른 속도와 그래픽 객체 처리 가능 덕분에, 이러한 아름다운 집합을 MetaTrader 5 클라이언트 터미널에서 연구할 수 있습니다.
cIntBMP 라이브러리는 새로운 그래픽 기회를 제공하며 그래픽 이미지를 만드는 과정을 크게 단순화해 줍니다. 이 라이브러리는 MetaQuotes Software Corp로부터 특별상을 수상했습니다.
이번 포스팅에서는 cIntBMP 라이브러리와 함께 작업하는 예제를 살펴보고, 반복 함수 시스템을 사용하여 프랙탈 집합을 생성하는 알고리즘을 다루겠습니다.
1. 평면의 아핀 변환
아핀 변환은 평면의 매핑을 의미합니다. 일반적으로 아핀 2D 변환은 어떤 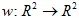 행렬과
행렬과 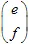 벡터로 정의될 수 있습니다. 좌표 (x,y)를 가진 점은 선형 변환을 통해 다른 점으로 변환됩니다:
벡터로 정의될 수 있습니다. 좌표 (x,y)를 가진 점은 선형 변환을 통해 다른 점으로 변환됩니다:
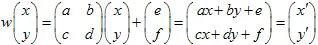
이 변환은 비특이적이어야 하며, 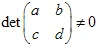 여야 합니다. 아핀 변환은 크기를
여야 합니다. 아핀 변환은 크기를 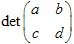 배 만큼 변경합니다.
배 만큼 변경합니다.
아핀 변환은 기하학적 객체의 구조를 변경하지 않으며 (선은 선으로 변환됨), 단순한 '변형'을 설명하는 데 사용됩니다. 예를 들어 회전, 크기 조정 및 이동이 있습니다.
아핀 평면 변환의 예:
1) 각도 로 평면 회전:
2) 평면의 크기 조정 (X 및 Y 축의
및
계수):
3) 벡터 에 의한 평면 이동:
수축 맵핑은 핵심입니다 (Hutchinson 결과 참조).
만약 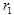 와
와 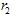 의 좌표가
의 좌표가 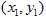 및
및 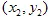 이고,
이고, 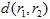 가 메트릭 (예: 유클리드 메트릭)이라면, 아핀 변환은 수축이라고 불립니다.
가 메트릭 (예: 유클리드 메트릭)이라면, 아핀 변환은 수축이라고 불립니다.
아핀 변환의 예시:

결과는 다음과 같습니다:
2. 유사 변환
프랙탈은 다음과 같이 구성됩니다: 어떤 (단순한) 기하학적 객체 (구역, 삼각형, 사각형)를 N 조각으로 나누고 그 중 M개를 사용하여 집합을 '구성'합니다 (N=M인 경우 결과 집합의 정수 차원을 얻게 됩니다). 이 과정은 각 조각에 대해 반복됩니다.
클래식 프랙탈:
구역:
- 삼중 코흐 곡선, N=3, M=4;
- 칸토르 먼지, N=3, M=2;
삼각형:
- 시어핀스키 기하, N=4, M=3;
사각형:
- 시어핀스키 카펫, N=9, M=8;
- 비체크 프랙탈, N=9, M=5.
계속해서.
프랙탈은 자기 유사 구조를 가지며, 일부는 여러 유사 변환으로 정의될 수 있습니다. 아핀 변환의 구조는 프랙탈 생성 방식에 따라 달라집니다.
여기서 보시게 될 것이지만, 이는 매우 간단하며, 우리가 해결해야 할 문제는 프랙탈 생성의 첫 번째 반복을 설명하고, 해당 아핀 변환 집합을 찾는 것입니다.
어떤 집합이 있다고 가정해 보겠습니다. 프랙탈 생성 알고리즘에 따라 이를 축소하고 회전시켜 '특정 위치에 놓아야' 합니다. 이 과정을 아핀 변환을 사용하여 설명해야 하므로, 행렬과 벡터를 찾아야 합니다.
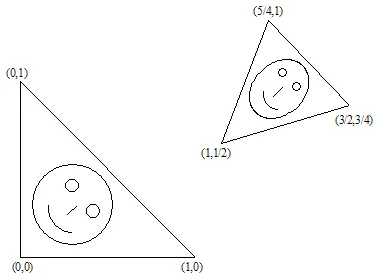
초기 집합의 3점을 취하는 것으로 충분하다는 것을 증명하기는 쉽습니다 (비자명한). 이 변환은 6개의 선형 방정식으로 이어지며, a, b, c, d, e, f를 해로 찾을 수 있습니다.
예를 들어 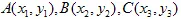 삼각형을
삼각형을 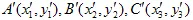 삼각형으로 변환한다고 가정합시다.
삼각형으로 변환한다고 가정합시다.
선형 방정식 시스템을 해결함으로써 a, b, c, d, e 및 f 계수를 얻을 수 있습니다:
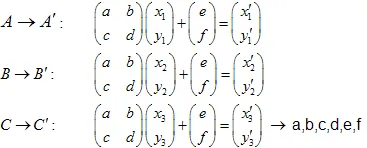
예시: 시어핀스키 기하:
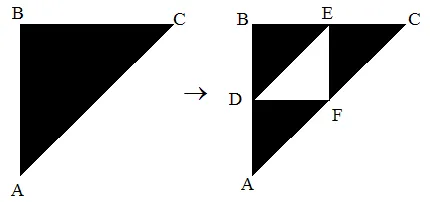
점의 좌표는 다음과 같습니다:
- A (0,0)
- B (0,1)
- C (1,1)
- D(0,1/2)
- E (1/2,1)
- F(1/2,1/2)
우리는 3가지 변환을 가집니다:
- ABC -> ADF
- ABC -> DBE
- ABC -> FEC
선형 방정식 시스템은 다음과 같습니다:
해는:  ,
, 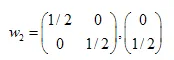 ,
, 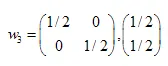
우리는 세 가지 아핀 변환의 계수를 찾았습니다. 이후 이를 자기 유사 집합을 생성하는 데 사용할 것입니다.
3. 반복 함수 시스템을 사용하여 프랙탈 생성하기
반복 함수 시스템(IFS)은 아핀 수축 집합의 모음입니다. 여기서 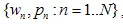 는 '가중치'입니다. 각 IFS 함수는 7개의 숫자로 정의됩니다:
는 '가중치'입니다. 각 IFS 함수는 7개의 숫자로 정의됩니다: 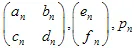 , 여기서
, 여기서 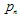 가 반복 과정에서 n번째 변환의 확률로 사용됩니다. 이 값을 수축에 비례하도록 정의하는 것이 좋습니다.
가 반복 과정에서 n번째 변환의 확률로 사용됩니다. 이 값을 수축에 비례하도록 정의하는 것이 좋습니다.
프랙탈을 생성하는 알고리즘을 살펴보겠습니다 (또한 혼돈 게임 참조).
먼저, 좌표 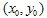 를 가진 초기 점을 선택합니다. 그 다음, 무작위로 수축 중 하나를 선택하고 점
를 가진 초기 점을 선택합니다. 그 다음, 무작위로 수축 중 하나를 선택하고 점 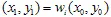 를 플로팅합니다. 다시 무작위로 수축 중 하나를 선택하고
를 플로팅합니다. 다시 무작위로 수축 중 하나를 선택하고 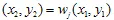 를 플로팅합니다. 최종적으로
를 플로팅합니다. 최종적으로 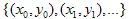 를 점 집합으로 가집니다.
를 점 집합으로 가집니다.
수축의 선택은 '확률'에 따라 다릅니다. 이 과정을 (~30000점) 반복하고 결과 집합을 플로팅하면, 무작위 과정에도 불구하고 그 구조를 볼 수 있습니다.
여기 시어핀스키 기하의 예시가 있습니다:
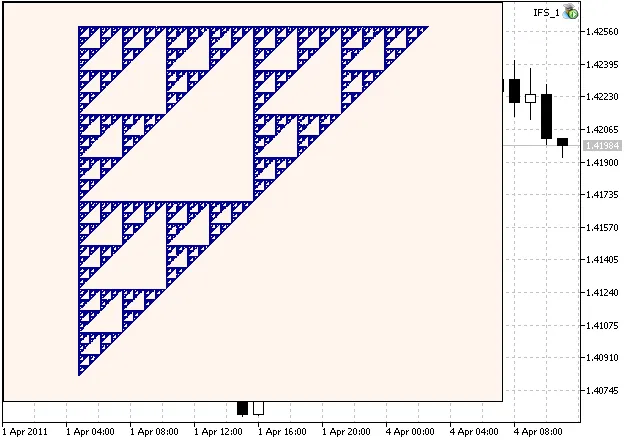
Figure 1. The Sierpinski Gasket, generated with IFS coefficients calculated in chapter 2
코드:
//+------------------------------------------------------------------+ //| IFS_Sierpinski_Gasket.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" //-- include file with cIntBMP class #include <cIntBMP.mqh> //-- Sierpinski Gasket IFS coefficients //-- (a,b,c,d) matricies double IFS_a[3] = {0.50, 0.50, 0.50}; double IFS_b[3] = {0.00, 0.00, 0.00}; double IFS_c[3] = {0.00, 0.00, 0.00}; double IFS_d[3] = {0.50, 0.50, 0.50}; //-- (e,f) vectors double IFS_e[3] = {0.00, 0.00, 0.50}; double IFS_f[3] = {0.00, 0.50, 0.50}; //-- "probabilities" of transforms, multiplied by 1000 double IFS_p[3]={333,333,333}; double Probs[3]; // Probs array - used to choose IFS transforms cIntBMP bmp; // cIntBMP class instance int scale=350; // scale coefficient //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //-- Prepare Probs array double m=0; for(int i=0; i<ArraySize(IFS_p); i++) { Probs[i]=IFS_p[i]+m; m=m+IFS_p[i]; } //-- size of BMP image int XSize=500; int YSize=400; //-- create bmp image XSizexYSize with clrSeashell background color bmp.Create(XSize,YSize,clrSeashell); //-- image rectangle bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack); //-- point coordinates (will be used in construction of set) double x0=0; double y0=0; double x,y; //-- number of points to calculate (more points - detailed image) int points=1500000; //-- calculate set for(int i=0; i<points; i++) { // choose IFS tranform with probabilities, proportional to defined double prb=1000*(rand()/32767.0); for(int k=0; k<ArraySize(IFS_p); k++) { if(prb<=Probs[k]) { // affine transformation x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k]; y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k]; // update previous coordinates x0 = x; y0 = y; // convert to BMP image coordinates // (note the Y axis in cIntBMP) int scX = int (MathRound(XSize/2 + (x-0.5)*scale)); int scY = int (MathRound(YSize/2 + (y-0.5)*scale)); // if the point coordinates inside the image, draw the dot if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrDarkBlue); } break; } } } //-- save image to file bmp.Save("bmpimg",true); //-- plot image on the chart bmp.Show(0,0,"bmpimg","IFS"); //--- return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- delete image from the chart ObjectDelete(0,"IFS"); //--- delete file bmp.Delete("bmpimg",true); } //+------------------------------------------------------------------+
스케일을 1350으로 설정하고 반복 횟수를 150000으로 늘리며 초기 점의 위치를 이동하면:
int scX = MathRound(XSize/2 + (x-0.75)*scale); int scY = MathRound(YSize/2 + (y-0.75)*scale);
우리는 집합의 확대된 영역을 볼 수 있습니다. 그 구조가 자기 유사적임을 알 수 있습니다:
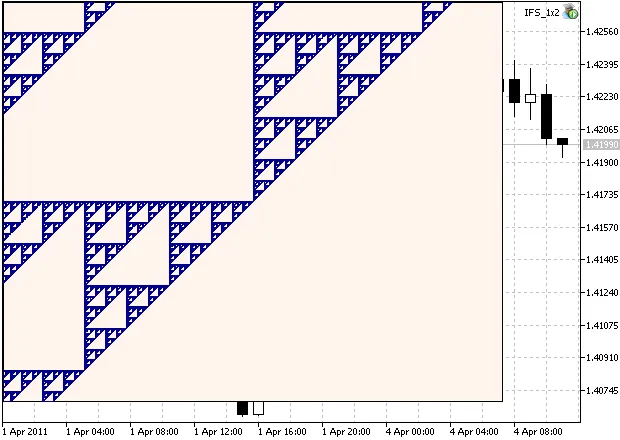
Figure 2. Zoomed region of Sierpinski Gasket
유명한 Barnsley의 양치식물를 고려해 보겠습니다. 이것은 더 복잡합니다.

Figure 3. Barnsley's Fern
코드는 비슷하지만, 이 경우에는 4개의 IFS 수축이 서로 다른 가중치로 존재합니다.
//+------------------------------------------------------------------+ //| IFS_fern.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #include <cIntBMP.mqh> //-- Barnsley Fern IFS coefficients //-- (a,b,c,d) matricies double IFS_a[4] = {0.00, 0.85, 0.20, -0.15}; double IFS_b[4] = {0.00, 0.04, -0.26, 0.28}; double IFS_c[4] = {0.00, -0.04, 0.23, 0.26}; double IFS_d[4] = {0.16, 0.85, 0.22, 0.24}; //-- (e,f) vectors double IFS_e[4] = {0.00, 0.00, 0.00, 0.00}; double IFS_f[4] = {0.00, 1.60, 1.60, 0.00}; //--

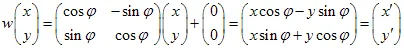
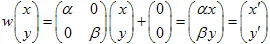
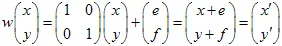
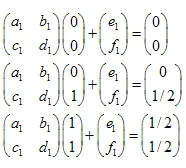

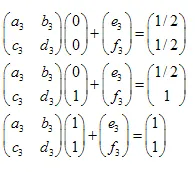
댓글 0