Introduction
Il existe de nombreux programmes permettant de créer des ensembles auto-similaires, définis par un Système de Fonctions Itérées (IFS). Par exemple, il y a Fractint, Fractal Designer ou encore IFS Matlab Generator. Grâce à la rapidité du langage MQL5 et à la possibilité de travailler avec des objets graphiques, ces magnifiques ensembles peuvent être étudiés directement dans le terminal client MetaTrader 5.
La bibliothèque cIntBMP, développée par Dmitry (Integer), offre de nouvelles opportunités graphiques et simplifie grandement la création d'images graphiques. Cette bibliothèque a été récompensée par un prix spécial par MetaQuotes Software Corp.
Dans cette publication, nous allons explorer des exemples d'utilisation de la bibliothèque cIntBMP. De plus, nous aborderons les algorithmes de création d'ensembles fractals en utilisant les Systèmes de Fonctions Itérées.
1. Transformation Affine du Plan
La transformation affine du plan est une cartographie 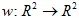 . En général, la transformation affine 2D peut être définie avec une matrice
. En général, la transformation affine 2D peut être définie avec une matrice 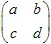 et un vecteur
et un vecteur 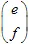 . Le point avec les coordonnées (x,y) se transforme en un autre point
. Le point avec les coordonnées (x,y) se transforme en un autre point 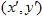 en utilisant la transformation linéaire :
en utilisant la transformation linéaire :
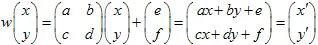
La transformation doit être non singulière, 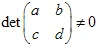 . La transformation affine change la taille
. La transformation affine change la taille 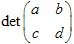 fois.
fois.
Les transformations affines ne changent pas la structure des objets géométriques (les lignes se transforment en lignes), et permettent de décrire de simples "déformations" des objets, telles que la rotation, le redimensionnement et la translation.
Exemples de transformations affines du plan :
1) Rotation du plan sur un angle:
2) Redimensionnement d'un plan avec des coefficients
et
(axes X et Y) :
3) Translation du plan par un vecteur
:
Les mappings de contraction sont la clé (voir les résultats de Hutchinson).
Si 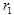 et
et 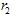 ont les coordonnées
ont les coordonnées 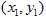 et
et 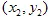 et
et 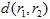 est une métrique (par exemple, la métrique euclidienne :
est une métrique (par exemple, la métrique euclidienne : 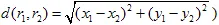 ). La transformation affine est appelée contraction si
). La transformation affine est appelée contraction si 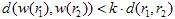 , où
, où 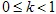 .
.
Voici un exemple de transformation affine :

Le résultat est :
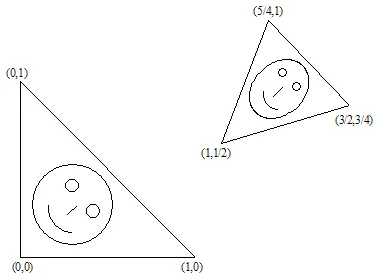
2. Transformations de Similarité
Les fractales sont construites de la manière suivante : un (simple) objet géométrique (section, triangle, carré) est divisé en N morceaux et M d'entre eux sont utilisés pour la "construction" ultérieure de l'ensemble (si N=M, nous obtiendrons la dimension entière de l'ensemble résultant). Ce processus est répété encore et encore pour chacun des morceaux.
Fractales classiques :
Sections :
- Courbe de Koch triadique, N=3, M=4;
- Poussière de Cantor, N=3, M=2;
Triangle :
- Gant de Sierpinski, N=4, M=3;
Carrés :
- Tapis de Sierpinski, N=9, M=8;
- Fractal de Vichek, N=9, M=5.
Et ainsi de suite.
Les fractales ont une structure auto-similaire, certaines d'entre elles peuvent être définies par plusieurs transformations de similarité. La structure de la transformation affine dépend de la manière dont la fractale est construite.
Comme vous le verrez plus loin, c'est très simple, et le seul problème que nous avons à résoudre est de décrire uniquement la première itération de la construction fractale et de trouver l'ensemble correspondant des transformations affines.
Supposons que nous avons un ensemble donné. Selon l'algorithme de création fractale, nous devons le réduire, le faire pivoter et le "placer à un certain endroit". Le problème consiste à décrire ce processus à l'aide de transformations affines, c'est-à-dire que nous devons trouver la matrice et le vecteur.
Il est facile de prouver qu'il suffit de prendre 3 points de l'ensemble initial (non triviaux) et de les transformer en 3 points correspondants de l'ensemble "réduit". Cette transformation aboutira à 6 équations linéaires, nous permettant de trouver les a, b, c, d, e et f en tant que solution.
Montrons cela. Supposons que 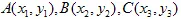 le triangle se transforme en
le triangle se transforme en 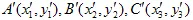 triangle.
triangle.
En résolvant le système d'équations linéaires, nous pourrons obtenir les coefficients a, b, c, d, e et f :
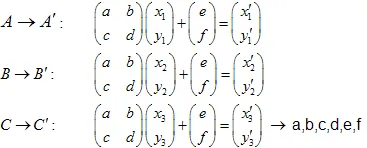
Exemple : Gant de Sierpinski :
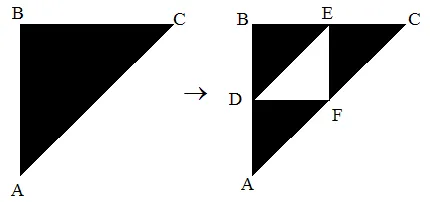
Les coordonnées des points sont :
- A (0,0)
- B (0,1)
- C (1,1)
- D(0,1/2)
- E (1/2,1)
- F(1/2,1/2)
Nous avons 3 transformations :
- ABC -> ADF
- ABC -> DBE
- ABC -> FEC
Le système d'équations linéaires ressemble à ceci :
Les solutions sont :  ,
, 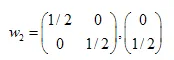 ,
, 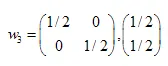
Nous avons trouvé les coefficients de trois transformations affines. Par la suite, nous les utiliserons pour créer des ensembles auto-similaires.
3. Création de Fractales avec les Systèmes de Fonctions Itérées
Le Système de Fonctions Itérées (IFS) est un ensemble de contractions affines 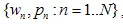 où
où 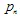 - est le "poids". Chacune des fonctions IFS est définie par 7 nombres :
- est le "poids". Chacune des fonctions IFS est définie par 7 nombres : 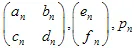 , où
, où 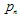 les poids sont utilisés lors du processus d'itération comme probabilité de la n-ième transformation. Il est préférable de définir leurs valeurs, proportionnelles à la contraction :
les poids sont utilisés lors du processus d'itération comme probabilité de la n-ième transformation. Il est préférable de définir leurs valeurs, proportionnelles à la contraction : 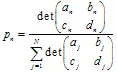 .
.
Considérons l'algorithme de construction de fractales utilisant le Système de Fonctions Itérées (voir aussi Jeu de Chaos).
Tout d'abord, nous avons besoin de prendre un point initial avec des coordonnées 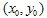 . Ensuite, nous choisissons aléatoirement une des contractions et traçons le point
. Ensuite, nous choisissons aléatoirement une des contractions et traçons le point 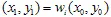 . Et encore, choisissons aléatoirement une des contractions
. Et encore, choisissons aléatoirement une des contractions 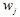 et traçons
et traçons  . Finalement, nous aurons l'
. Finalement, nous aurons l' comme un ensemble de points.
comme un ensemble de points.
Le choix de la contraction dépend de sa "probabilité". Si nous répétons le processus (par exemple, environ 30 000 points) et traçons l'ensemble résultant, nous verrons sa structure malgré le processus aléatoire.
Voici un exemple du Gant de Sierpinski :

Figure 1. Le Gant de Sierpinski, généré avec des coefficients IFS calculés au chapitre 2
Le code :
//+------------------------------------------------------------------+ //| IFS_Sierpinski_Gasket.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" //-- include file with cIntBMP class #include <cIntBMP.mqh> //-- Sierpinski Gasket IFS coefficients //-- (a,b,c,d) matricies double IFS_a[3] = {0.50, 0.50, 0.50}; double IFS_b[3] = {0.00, 0.00, 0.00}; double IFS_c[3] = {0.00, 0.00, 0.00}; double IFS_d[3] = {0.50, 0.50, 0.50}; //-- (e,f) vectors double IFS_e[3] = {0.00, 0.00, 0.50}; double IFS_f[3] = {0.00, 0.50, 0.50}; //-- "probabilities" of transforms, multiplied by 1000 double IFS_p[3]={333,333,333}; double Probs[3]; // Probs array - used to choose IFS transforms cIntBMP bmp; // cIntBMP class instance int scale=350; // scale coefficient //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //-- Prepare Probs array double m=0; for(int i=0; i<ArraySize(IFS_p); i++) { Probs[i]=IFS_p[i]+m; m=m+IFS_p[i]; } //-- size of BMP image int XSize=500; int YSize=400; //-- create bmp image XSizexYSize with clrSeashell background color bmp.Create(XSize,YSize,clrSeashell); //-- image rectangle bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack); //-- point coordinates (will be used in construction of set) double x0=0; double y0=0; double x,y; //-- number of points to calculate (more points - detailed image) int points=1500000; //-- calculate set for(int i=0; i<points; i++) { // choose IFS tranform with probabilities, proportional to defined double prb=1000*(rand()/32767.0); for(int k=0; k<ArraySize(IFS_p); k++) { if(prb<=Probs[k]) { // affine transformation x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k]; y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k]; // update previous coordinates x0 = x; y0 = y; // convert to BMP image coordinates // (note the Y axis in cIntBMP) int scX = int (MathRound(XSize/2 + (x-0.5)*scale)); int scY = int (MathRound(YSize/2 + (y-0.5)*scale)); // if the point coordinates inside the image, draw the dot if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrDarkBlue); } break; } } } //-- save image to file bmp.Save("bmpimg",true); //-- plot image on the chart bmp.Show(0,0,"bmpimg","IFS"); //--- return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- delete image from the chart ObjectDelete(0,"IFS"); //--- delete file bmp.Delete("bmpimg",true); } //+------------------------------------------------------------------+
Si nous définissons l'échelle à 1350, augmentons le nombre d'itérations à 15 000 000 et modifions le décalage du point initial :
int scX = MathRound(XSize/2 + (x-0.75)*scale); int scY = MathRound(YSize/2 + (y-0.75)*scale);
nous pourrons voir la région zoomée de l'ensemble. On peut voir (Fig. 2), qu'elle a une structure auto-similaire :

Figure 2. Région zoomée du Gant de Sierpinski
Considérons la célèbre Fougère de Barnsley, proposée par Michael Barnsley. Elle est plus complexe.

Figure 3. Fougère de Barnsley
Le code est similaire, mais dans ce cas, nous avons 4 contractions IFS avec des poids différents.
//+------------------------------------------------------------------+ //| IFS_fern.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #include <cIntBMP.mqh> //-- Barnsley Fern IFS coefficients //-- (a,b,c,d) matricies double IFS_a[4] = {0.00, 0.85, 0.20, -0.15}; double IFS_b[4] = {0.00, 0.04, -0.26, 0.28}; double IFS_c[4] = {0.00, -0.04, 0.23, 0.26}; double IFS_d[4] = {0.16, 0.85, 0.22, 0.24}; //-- (e,f) vectors double IFS_e[4] = {0.00, 0.00, 0.00, 0.00}; double IFS_f[4] = {0.00, 1.60, 1.60, 0.00}; //-- "probabilities" of transforms, multiplied by 1000 double IFS_p[4] = {10, 850, 70, 70}; double Probs[4]; cIntBMP bmp; int scale=50; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { double m=0; for(int i=0; i<ArraySize(IFS_p); i++) { Probs[i]=IFS_p[i]+m; m=m+IFS_p[i]; } int XSize=600; int YSize=600; bmp.Create(XSize,YSize,clrSeashell); bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack); double x0=0; double y0=0; double x,y; int points=250000; for(int i=0; i<points; i++) { double prb=1000*(rand()/32767.0); for(int k=0; k<ArraySize(IFS_p); k++) { if(prb<=Probs[k]) { x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k]; y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k]; x0 = x; y0 = y; int scX = int (MathRound(XSize/2 + (x-0.75)*scale)); int scY = int (MathRound(YSize/2 + (y-0.75)*scale)); if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrForestGreen); } break; } } } bmp.Save("bmpimg",true); bmp.Show(0,0,"bmpimg","IFS"); //--- return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { ObjectDelete(0,"IFS"); bmp.Delete("bmpimg",true); } //+------------------------------------------------------------------+
Il est remarquable que cette structure complexe puisse être définie par seulement 28 nombres.
Si nous augmentons l'échelle à 150, et définissons les itérations à 1 250 000, nous verrons un fragment zoomé :

Figure 4. Un fragment de la Fougère de Barnsley
Comme vous pouvez le voir, l'algorithme est universel, il permet de générer différents ensembles fractals.
Examinons le Tapis de Sierpinski, défini par les coefficients IFS suivants :
//-- Sierpinski Gasket IFS coefficients double IFS_a[8] = {0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333}; double IFS_b[8] = {0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00}; double IFS_c[8] = {0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00}; double IFS_d[8] = {0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333}; double IFS_e[8] = {-0.125, -3.375, -3.375, 3.125, 3.125, -3.375, -0.125, 3.125}; double IFS_f[8] = {6.75, 0.25, 6.75, 0.25, 6.75, 3.5, 0.25, 3.50}; //-- "probabilities", multiplied by 1000 double IFS_p[8]={125,125,125,125,125,125,125,125};

Figure 5. Tapis de Sierpinski
Au chapitre 2, nous avons considéré l'algorithme de calcul des coefficients des contractions IFS.
Examinons comment créer des "mots fractals". En russe, le mot "Fractals" s'écrit comme suit :

Figure 6. Mot "fractals" en russe
Pour trouver les coefficients IFS, nous devons résoudre les systèmes linéaires correspondants. Les solutions sont :
//-- IFS coefficients of the 
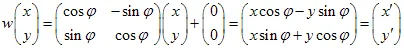
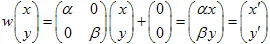
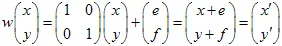
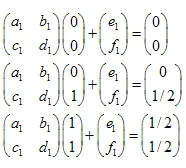

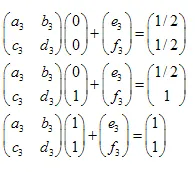
Commentaire 0