Inleiding
Er zijn verschillende programma's beschikbaar waarmee je zelf-similaire verzamelingen kunt creëren, gedefinieerd door het Iterated Function System (IFS). Een paar voorbeelden hiervan zijn Fractint, Fractal Designer en IFS Matlab Generator. Met de snelheid van de MQL5 taal en de mogelijkheid om met grafische objecten te werken, kunnen deze prachtige verzamelingen bestudeerd worden in de MetaTrader 5 client terminal.
De cIntBMP bibliotheek, ontwikkeld door Dmitry (Integer), biedt nieuwe grafische mogelijkheden en vereenvoudigt het creëren van grafische afbeeldingen aanzienlijk. Deze bibliotheek is bekroond met een speciale prijs van MetaQuotes Software Corp.
In deze publicatie bekijken we voorbeelden van het werken met de cIntBMP bibliotheek. Daarnaast behandelen we de algoritmes voor het creëren van fractale verzamelingen met behulp van de Iterated Function Systems.
1. Affiene Transformatie van het Vlak
De affiene transformatie van een vlak is een mapping 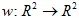 . Over het algemeen kan de affiene 2D transformatie gedefinieerd worden met een
. Over het algemeen kan de affiene 2D transformatie gedefinieerd worden met een 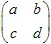 matrix en een
matrix en een 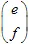 , vector. Een punt met coördinaten (x,y) transformeert naar een ander punt
, vector. Een punt met coördinaten (x,y) transformeert naar een ander punt 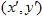 met behulp van de lineaire transformatie:
met behulp van de lineaire transformatie:
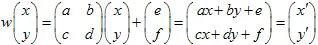
De transformatie moet niet-singulier zijn, de 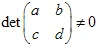 . De affiene transformatie verandert de grootte
. De affiene transformatie verandert de grootte 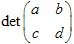 keer.
keer.
Affiene transformaties veranderen de structuur van geometrische objecten niet (lijnen worden in lijnen getransformeerd), de AT maakt het mogelijk om eenvoudige "deformaties" van de objecten te beschrijven, zoals rotatie, schaling en translatie.
Voorbeelden van affiene vlaktransformaties:
1) Rotatie van het vlak onder eenhoek:
2) "Schaling van een vlak" met
en
coëfficiënten (X- en Y-assen):
3) Translatie van het vlak door een
vector:
De contractie mappings is de sleutel (zie Hutchinson resultaten).
Als 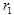 en
en 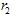 coördinaten hebben
coördinaten hebben 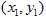 en
en 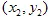 en
en 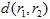 is een metriek (bijvoorbeeld, Euclidische metriek:
is een metriek (bijvoorbeeld, Euclidische metriek: 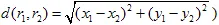 ). De affiene transformatie wordt contractie genoemd als
). De affiene transformatie wordt contractie genoemd als 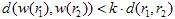 , waar
, waar 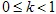 .
.
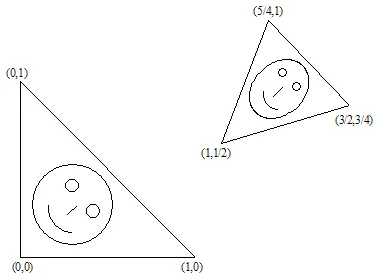
Hier is een voorbeeld van een affiene transformatie:

Het resultaat is:
2. Gelijkenistransformaties
De fractalen worden op de volgende manier geconstrueerd: een (eenvoudig) geometrisch object (sectie, driehoek, vierkant) wordt verdeeld in N stukken en M ervan worden gebruikt voor verdere "constructie" van de verzameling (als N=M, krijgen we de gehele dimensie van de resulterende verzameling). Dit proces wordt herhaald voor elk van de stukken.
Classic fractalen:
Secties:
- Triadische Koch Curve, N=3, M=4;
- Cantor Dust, N=3, M=2;
Driehoek:
- Sierpinski Gasket, N=4, M=3;
Vierkanten:
- Sierpinski Carpet, N=9, M=8;
- Vichek fractal, N=9, M=5.
enzovoorts.
De fractalen hebben een zelf-similaire structuur en sommige kunnen gedefinieerd worden door verschillende gelijkenistransformaties. De structuur van de affiene transformatie hangt af van de manier waarop de fractal is geconstrueerd.
Zoals je verder zult zien, is het heel eenvoudig, en het enige dat we moeten oplossen, is het beschrijven van alleen de eerste iteratie van de fractalconstructie en het vinden van de bijbehorende set affiene transformaties.
Stel dat we een bepaalde set hebben. Volgens het algoritme voor het maken van fractalen moeten we deze verkleinen, draaien en "op een bepaalde plaats zetten". Het probleem is dit proces te beschrijven met behulp van affiene transformaties, dat wil zeggen, we moeten de matrix en vector vinden.
Het is eenvoudig te bewijzen dat het voldoende is om 3 punten van de initiële set (niet-triviaal) te nemen en deze te transformeren naar 3 bijbehorende punten van de "verkleinde" set. Deze transformatie zal leiden tot 6 lineaire vergelijkingen, waardoor we de a,b,c,d,e,f als oplossing kunnen vinden.
Laten we dit tonen. Stel dat de 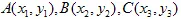 driehoek omgevormd wordt naar de
driehoek omgevormd wordt naar de 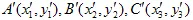 driehoek.
driehoek.
Door het oplossen van het systeem van lineaire vergelijkingen kunnen we de a,b,c,d,e en f coëfficiënten krijgen:
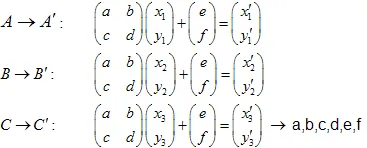
Voorbeeld: Sierpinski Gasket:
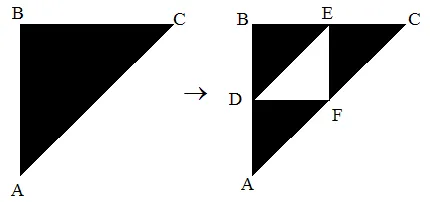
De coördinaten van de punten zijn:
- A (0,0)
- B (0,1)
- C (1,1)
- D(0,1/2)
- E (1/2,1)
- F(1/2,1/2)
We hebben 3 transformaties:
- ABC -> ADF
- ABC -> DBE
- ABC -> FEC
Het systeem van lineaire vergelijkingen ziet er als volgt uit:
De oplossingen zijn:  ,
, 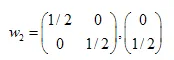 ,
, 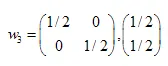
We hebben de coëfficiënten van drie affiene transformaties gevonden. Verder zullen we ze gebruiken voor het creëren van zelf-similaire sets.
3. Fractalen Creëren met de Iterated Function Systems
Het Iterated Function System (IFS) is een set van affiene contracties 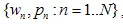 waar
waar 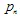 - zijn de "gewichten". Elke IFS functie is gedefinieerd door 7 getallen:
- zijn de "gewichten". Elke IFS functie is gedefinieerd door 7 getallen: 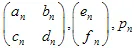 , waar
, waar 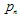 gewichten worden gebruikt tijdens het iteratieproces als een kans voor de n-de transformatie. Het is beter om hun waarden te definiëren, proportioneel aan de contractie:
gewichten worden gebruikt tijdens het iteratieproces als een kans voor de n-de transformatie. Het is beter om hun waarden te definiëren, proportioneel aan de contractie: 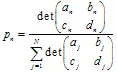 .
.
Laten we het algoritme voor het construeren van fractalen bekijken met behulp van het Iterated Function System (zie ook Chaos Game).
Als eerste nemen we een bepaald startpunt met coördinaten 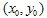 . Vervolgens kiezen we willekeurig een van de contracties en plotten het punt
. Vervolgens kiezen we willekeurig een van de contracties en plotten het punt 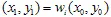 . En nogmaals, laten we willekeurig een van de contracties
. En nogmaals, laten we willekeurig een van de contracties 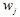 kiezen en plotten
kiezen en plotten 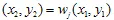 . Uiteindelijk zullen we de
. Uiteindelijk zullen we de 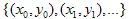 als een set van punten hebben.
als een set van punten hebben.
De keuze van contractie hangt af van de "kans". Als we het proces herhalen (bijvoorbeeld, tot ~30000 punten) en de resulterende set plotten, zullen we de structuur zien ondanks het willekeurige proces.
Hier is een voorbeeld van de Sierpinski Gasket:
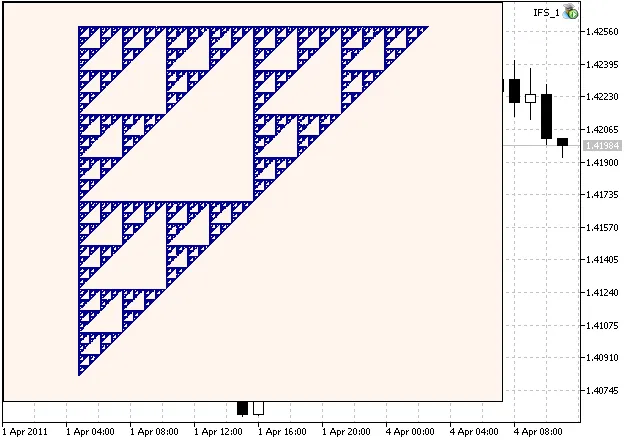
Figuur 1. De Sierpinski Gasket, gegenereerd met IFS-coëfficiënten berekend in hoofdstuk 2
De code:
//+------------------------------------------------------------------+ //| IFS_Sierpinski_Gasket.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" //-- include file with cIntBMP class #include <cIntBMP.mqh> //-- Sierpinski Gasket IFS coëfficiënten //-- (a,b,c,d) matrices double IFS_a[3] = {0.50, 0.50, 0.50}; double IFS_b[3] = {0.00, 0.00, 0.00}; double IFS_c[3] = {0.00, 0.00, 0.00}; double IFS_d[3] = {0.50, 0.50, 0.50}; //-- (e,f) vectors double IFS_e[3] = {0.00, 0.00, 0.50}; double IFS_f[3] = {0.00, 0.50, 0.50}; //--

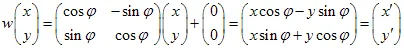
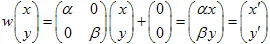
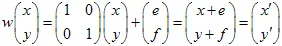
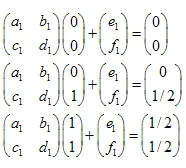

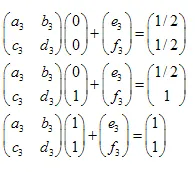
Reactie 0